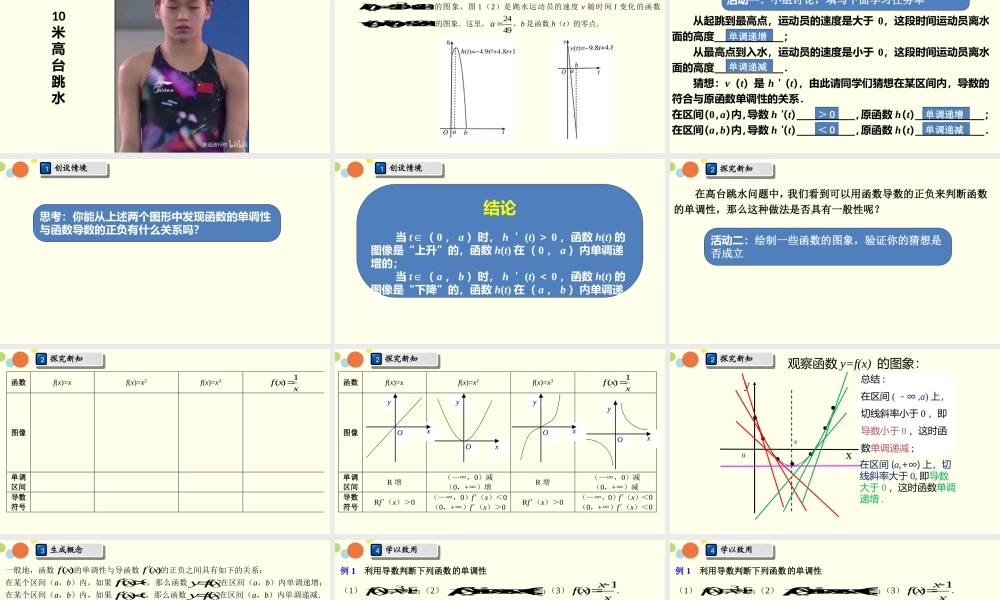
函数的单调性与导数1创设情境10米高台跳水图1(1)是某高台跳水运动员的重心相对于水面的高度h随时间t变化的函数2()4.94.811httt的图象,图1(2)是跳水运动员的速度v随时间l变化的函数()'()9.84.8vthtt的图象.这里,2449a,b是函数h(t)的零点.1创设情境1创设情境从起跳到最高点,运动员的速度是大于0,这段时间运动员离水面的高度;从最高点到入水,运动员的速度是小于0,这段时间运动员离水面的高度.猜想:v(t)是h'(t),由此请同学们猜想在某区间内,导数的符合与原函数单调性的关系.在区间(0,a)内,导数h'(t),原函数h(t);在区间(a,b)内,导数h'(t),原函数h(t).活动一:小组讨论,填写下面学习任务单单调递增单调递减>0<0单调递增单调递减1创设情境思考:你能从上述两个图形中发现函数的单调性与函数导数的正负有什么关系吗?1创设情境结论当t∈(0,a)时,h'(t)>0,函数h(t)的图像是“上升”的,函数h(t)在(0,a)内单调递增的;当t∈(a,b)时,h'(t)<0,函数h(t)的图像是“下降”的,函数h(t)在(a,b)内单调递减的.活动二:绘制一些函数的图象,验证你的猜想是否成立2探究新知在高台跳水问题中,我们看到可以用函数导数的正负来判断函数的单调性,那么这种做法是否具有一般性呢?2探究新知函数f(x)=xf(x)=x2f(x)=x31()fxx图像单调区间导数符号2探究新知函数f(x)=xf(x)=x2f(x)=x31()fxx图像单调区间R增(—∞,0)减(0,+∞)增R增(—∞,0)减(0,+∞)减导数符号Rf'(x)>0(—∞,0)f'(x)<0(0,+∞)f'(x)>0Rf'(x)>0(—∞,0)f'(x)<0(0,+∞)f'(x)<0OyxOyxOyxOyxayx0.......观察函数y=f(x)的图象:总结:在区间(-∞,a)上,切线斜率小于0,即导数小于0,这时函数单调递减;在区间(a,+∞)上,切线斜率大于0,即导数大于0,这时函数单调递增.2探究新知aby=f(x)xoyy=f(x)xoyabf'(x)>0f'(x)<0如果在某个区间内恒有f′(x)=0,则f(x)为常数.3生成概念一般地,函数()fx的单调性与导函数()fx的正负之间具有如下的关系:在某个区间(a,b)内,如果()0fx,那么函数()yfx在区间(a,b)内单调递增;在某个区间(a,b)内,如果()0fx,那么函数()yfx在区间(a,b)内单调递减.4学以致用例1利用导数判断下列函数的单调性(1)3()3fxxx;(2)()sin(0,)fxxxx,;(3)1()xfxx.解:(1)因为3()3fxxx,所以22()33=31f...