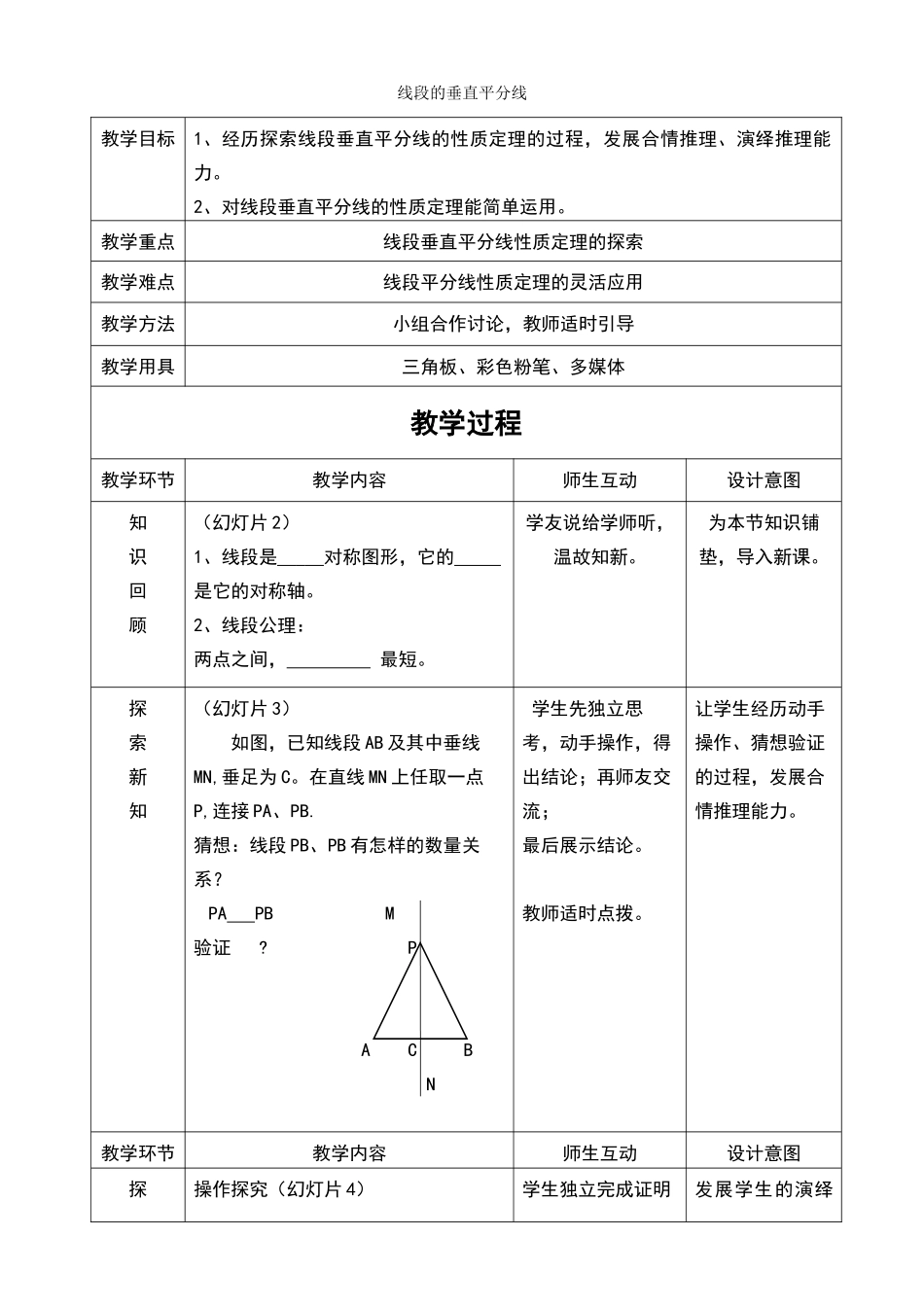
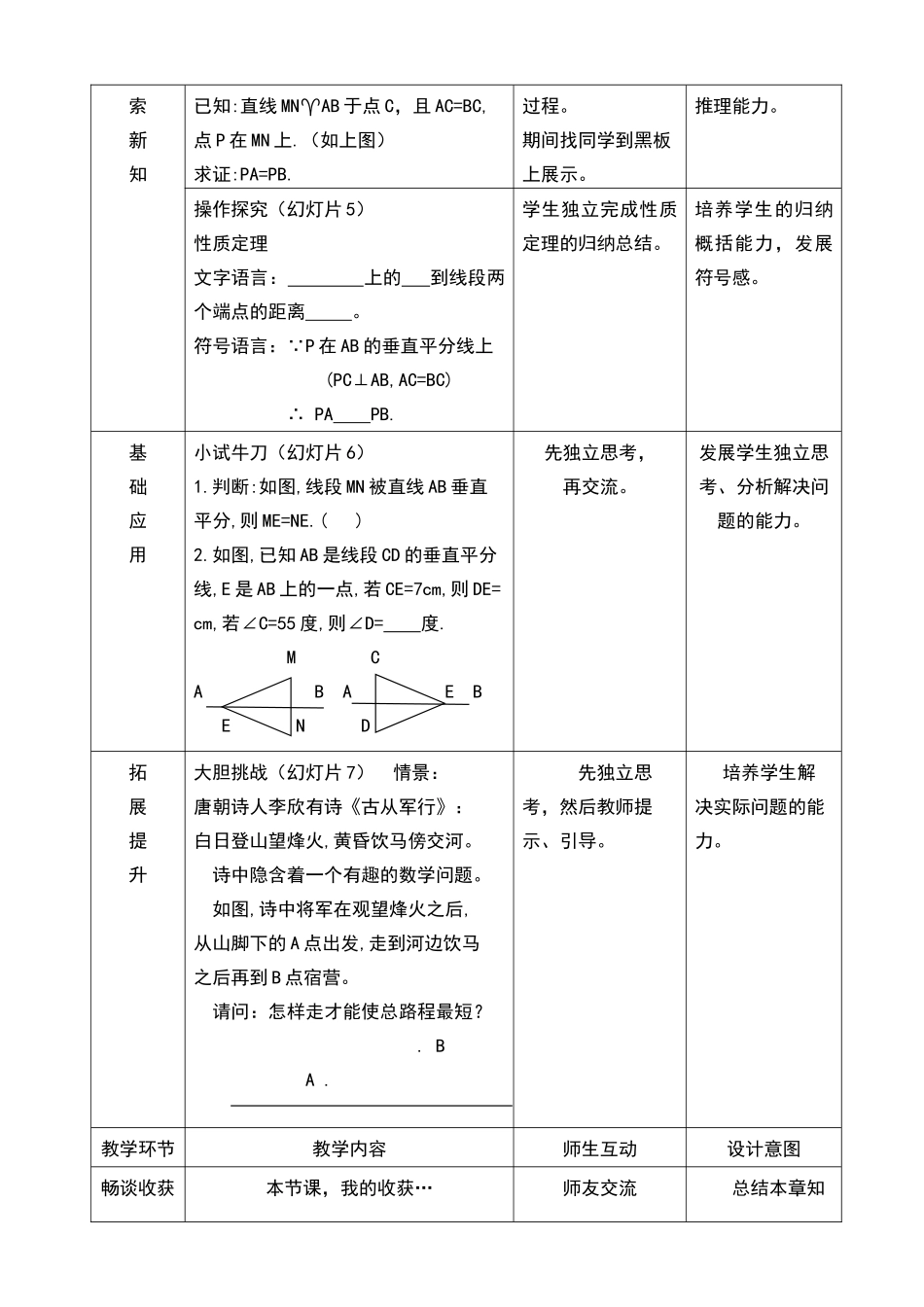
线段的垂直平分线教学目标1、经历探索线段垂直平分线的性质定理的过程,发展合情推理、演绎推理能力。2、对线段垂直平分线的性质定理能简单运用。教学重点线段垂直平分线性质定理的探索教学难点线段平分线性质定理的灵活应用教学方法小组合作讨论,教师适时引导教学用具三角板、彩色粉笔、多媒体教学过程教学环节教学内容师生互动设计意图知识回顾(幻灯片2)1、线段是对称图形,它的是它的对称轴。2、线段公理:两点之间,最短。学友说给学师听,温故知新。为本节知识铺垫,导入新课。探索新知(幻灯片3)如图,已知线段AB及其中垂线MN,垂足为C。在直线MN上任取一点P,连接PA、PB.猜想:线段PB、PB有怎样的数量关系?PAPBM验证?PACBN学生先独立思考,动手操作,得出结论;再师友交流;最后展示结论。教师适时点拨。让学生经历动手操作、猜想验证的过程,发展合情推理能力。教学环节教学内容师生互动设计意图探操作探究(幻灯片4)学生独立完成证明发展学生的演绎索新知已知:直线MNAB于点C,且AC=BC,点P在MN上.(如上图)求证:PA=PB.过程。期间找同学到黑板上展示。推理能力。操作探究(幻灯片5)性质定理文字语言:上的到线段两个端点的距离。符号语言:∵P在AB的垂直平分线上(PC⊥AB,AC=BC)∴PAPB.学生独立完成性质定理的归纳总结。培养学生的归纳概括能力,发展符号感。基础应用小试牛刀(幻灯片6)1.判断:如图,线段MN被直线AB垂直平分,则ME=NE.()2.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,若CE=7cm,则DE=cm,若∠C=55度,则∠D=度.MCABAEBEND先独立思考,再交流。发展学生独立思考、分析解决问题的能力。拓展提升大胆挑战(幻灯片7)情景:唐朝诗人李欣有诗《古从军行》:白日登山望烽火,黄昏饮马傍交河。诗中隐含着一个有趣的数学问题。如图,诗中将军在观望烽火之后,从山脚下的A点出发,走到河边饮马之后再到B点宿营。请问:怎样走才能使总路程最短?.BA.先独立思考,然后教师提示、引导。培养学生解决实际问题的能力。教学环节教学内容师生互动设计意图畅谈收获本节课,我的收获…师友交流总结本章知识点,强化理解本章重点、跟踪检测小试牛刀(幻灯片9)已知:如图,D、E分别是AB、AC的中点,CD⊥AB于点D,BE⊥AC于点E。求证:AC=ABCEADB先独立思考,然后交流。提高学生分析问题的能力。布置作业学案:课后作业课本:必做A组选做B组板书设计16.2线段的垂直平分线(1)性质定理:应用:.BA.证明:课后反思