4.4.3 对数函数（第三课时课件）-2023-2024学年高一数学同步备课《知识•素养•思维》精讲课件（人教A版2019必修第一册）.pptxVIP免费

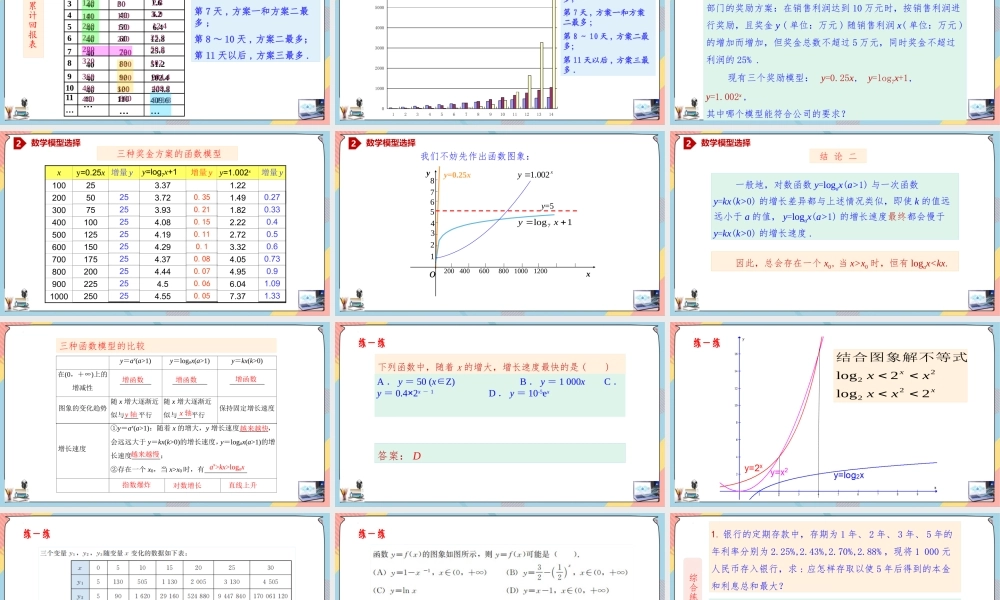
第四章指数函数与对数函数4.4.3不同函数增长的差异高中数学/人教A版/必修一……知识篇素养篇思维篇4.4.3不同函数增长的差异在前面的学习中我们看到，一次函数与指数函数的增长方式存在很大差异．事实上，这种差异正是不同类型现实问题具有不同增长规律的反映．因此，如果把握了不同函数增长方式的差异，那么就可以根据现实问题的增长情况，选择合适的函数模型刻画其变化规律．下面就来研究一次函数、指数函数和对数函数增长方式的差异．假设你有一笔资金用于投资，有三种投资方案供你选择，这三种方案的回报如下：方案一：每天回报40元；方案二：第一天回报10元，以后每天比前一天多回报10元；方案三：第一天回报0.4元，以后每天的回报比前一天翻一番.你会选择哪种投资方案呢？1比较案例9345786121030…方案三x/天方案一方案二y=40y=10xy=0.4×2x-1903040507080601020100300…4040404040404040404040…0.40.81.63.2…204.8102.4214748364.86.451.225.612.8每天回报表从每天的回报量看：第1～3天,方案一最多；第4天,方案一和方案二最多;第5～8天,方案二最多；第９天以后,方案三最多.结论1比较案例x/天方案一y=40方案二y=10x方案三y=0.4×2x-1y/元增长量/元y/元增长量/元y/元增长量/元140100.4240200.8340301.6440540640740840940…………3040300214748364.84050607080903.26.412.825.651.2102.400000000…01010101010101010…100.40.81.63.26.412.825.651.2…107374182.4零增长匀速增长急速增长1比较案例列表法比较三种方案“指数爆炸”12346578910200406080100120140yx方案一:y=401234567891040404040404040404040x方案二y=10x12345678910102030405060708090100xy=0.4·2x-1123456789100.40.81.63.26.412.825.651.2102.4204.8从每天的回报量来看：第______天，方案一最多：第______天，方案二最多：第______天以后，方案三最多；1~44~89y=0.4·2x-1y=10x1比较案例图象法比较三种方案y=40读图和用图具体来说，尽管方案一、方案二在第1天所得回报分别是方案三的100倍和25倍，但它们的增长量固定不变，而方案三是“指数增长”，其增长量是成倍增加的，从第7天开始，方案三比其他两个方案增长得快得多.这种增长速度是方案一、方案二所无法企及的.由表和图可知：方案一的函数是常数函数，方案二、方案三的函数都是增函数，但二者增长情况很不相同.1比较案例一般地，指数函数y=ax(a>1)与一次...