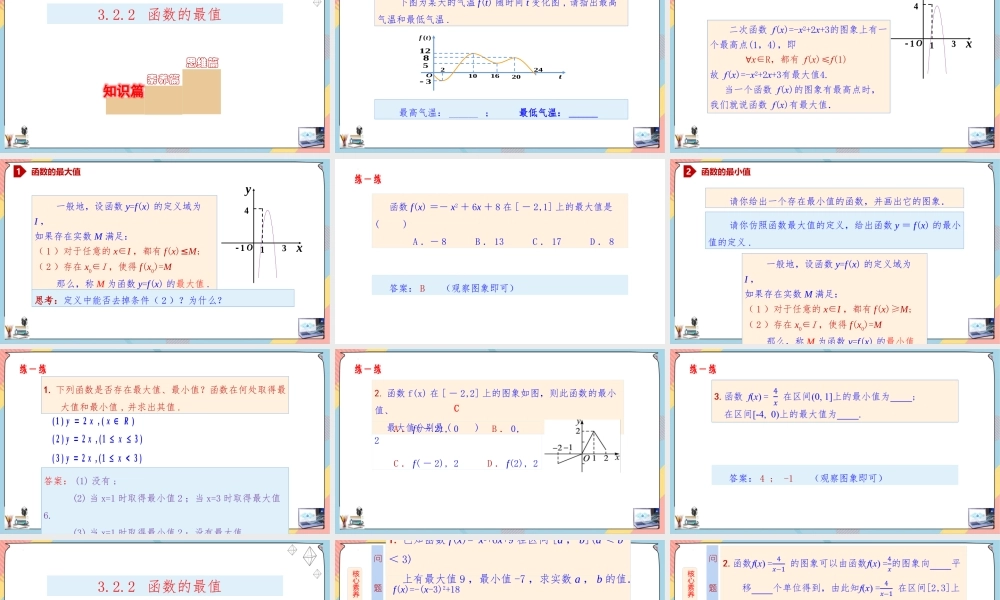
第三章函数的概念与性质3.2.2函数的最值高中数学/人教A版/必修一知识篇素养篇思维篇3.2.2函数的最值t()ftO24102016235128下图为某天的气温f(t)随时间t变化图,请指出最高气温和最低气温.最高气温:______;最低气温:______xyO13141函数的最大值1函数的最大值一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:(1)对于任意的x∈I,都有f(x)≤M;(2)存在x0∈I,使得f(x0)=M那么,称M为函数y=f(x)的最大值.思考:定义中能否去掉条件(2)?为什么?xyO1314练一练函数f(x)=-x2+6x+8在[-2,1]上的最大值是()A.-8B.13C.17D.8答案:B(观察图象即可)请你给出一个存在最小值的函数,并画出它的图象.2函数的最小值请你仿照函数最大值的定义,给出函数y=f(x)的最小值的定义.一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:(1)对于任意的x∈I,都有f(x)≥M;(2)存在x0∈I,使得f(x0)=M那么,称M为函数y=f(x)的最小值1.下列函数是否存在最大值、最小值?函数在何处取得最大值和最小值,并求出其值.(1)2,()yxxR(2)2,(13)yxx(3)2,(13)yxx答案:(1)没有;(2)当x=1时取得最小值2;当x=3时取得最大值6.(3)当x=1时取得最小值2;没有最大值练一练练一练2.函数f(x)在[-2,2]上的图象如图,则此函数的最小值、最大值分别是()A.f(-2),0B.0,2C.f(-2),2D.f(2),2C练一练答案:4;-1(观察图象即可)知识篇素养篇思维篇3.2.2函数的最值1.已知函数f(x)=x2+6x+9在区间[a,b](a<b<3)上有最大值9,最小值-7,求实数a,b的值.1.利用二次函数的性质(配方法)求函数的最大(小)值;2利用图象求函数的最大(小)值f(x)=-(x-3)2+18因为a<b<3,所以当x=a时,函数取得最小值ymin=-7;当x=b时,函数取得最大值ymax=9;即解得:a=8或-2;b=0或6.又因为a<b<3,所以a=-2;b=0.22a6a97,b6b99,==方法总结核心素养之逻辑推理+数学运算问题解析右;1;4;2(结合图象即可)如果函数y=f(x)在区间[a,b]上单调递增,则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b);如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增,则函数y=f(x)在x=b处有最小值f(b).方法总结核心素养之逻辑推理+数学运算问题答案3.“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度h(m)与时间t(s)之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂...