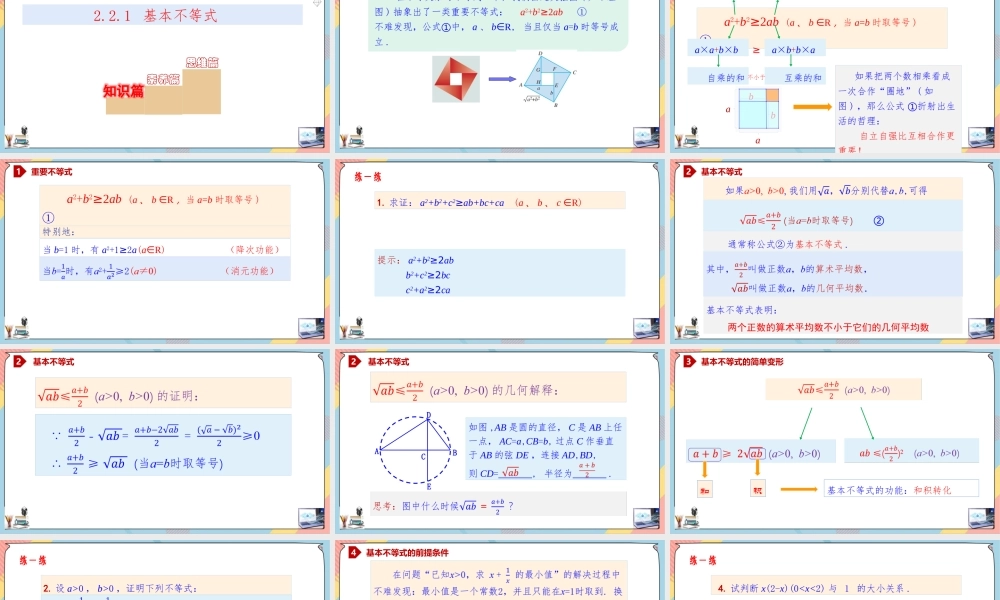
第二章一元二次函数、方程、不等式2.2.1基本不等式高中数学/人教A版/必修一知识篇素养篇思维篇2.2.1基本不等式在不等关系与不等式一节,我们由赵爽弦图(如下左图)抽象出了一类重要不等式:a2+b2≥2ab①不难发现,公式①中,a、b∈R,当且仅当a=b时等号成立.a2+b2≥2ab(a、b∈R,当a=b时取等号)①a×a+b×ba×b+b×a≥二次式二次式自乘的和互乘的和不小于如果把两个数相乘看成一次合作“圈地”(如图),那么公式①折射出生活的哲理:自立自强比互相合作更重要!重要不等式1aabb特别地:a2+b2≥2ab(a、b∈R,当a=b时取等号)①重要不等式1当b=1时,有a2+1≥2a(a∈R)(降次功能)1.求证:a2+b2+c2≥ab+bc+ca(a、b、c∈R)练一练提示:a2+b2≥2abb2+c2≥2bcc2+a2≥2ca基本不等式2基本不等式表明:两个正数的算术平均数不小于它们的几何平均数通常称公式②为基本不等式.基本不等式2基本不等式2DABCE如图,AB是圆的直径,C是AB上任一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连接AD,BD,则CD=,半径为.基本不等式的简单变形3和积基本不等式的功能:和积转化练一练2.设a>0,b>0,证明下列不等式:基本不等式的前提条件4练一练4.试判断x(2-x)(0