5.4.2.1 正弦函数、余弦函数的性质（一）（课件）-2023-2024学年高一数学同步备课《知识•素养•思维》精讲课件（人教A版2019必修第一册）.pptxVIP免费

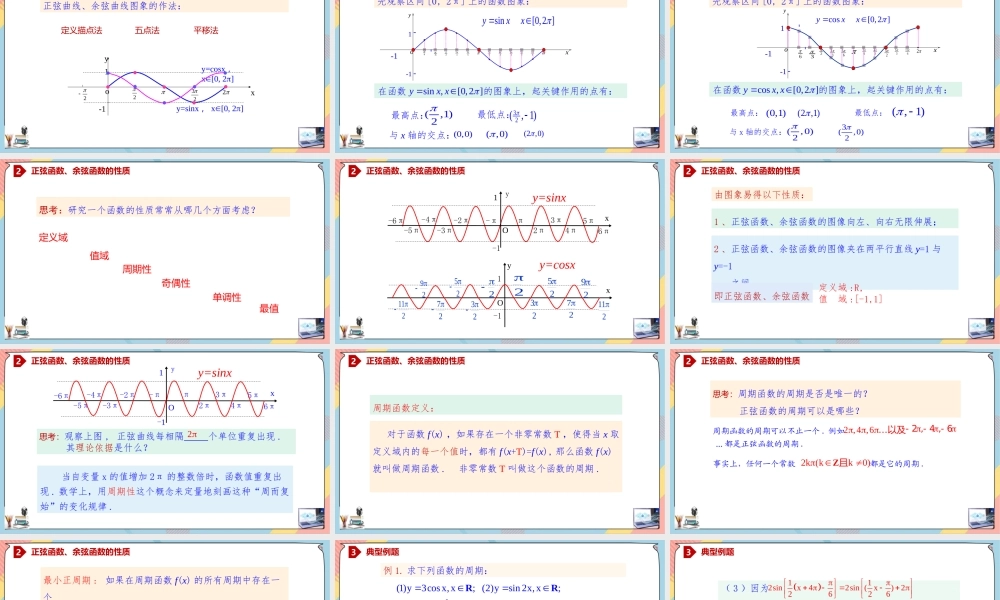
第五章三角函数5.4.2.1正弦函数、余弦函数的性质(一)高中数学/人教A版/必修一正弦曲线、余弦曲线图象的作法：yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]平移法定义描点法五点法1复习回顾先观察区间[0,2π]上的函数图象：2oxy---11--13232656734233561126sin[0,2]yxx在函数的图象上，起关键作用的点有：sin,[0,2]yxx最高点：最低点：与x轴的交点：(0,0)(,0)(2,0)32(,1)(,1)22正弦函数、余弦函数的性质-oxy---11--13232656734233561126cos[0,2]yxx最高点：最低点：与x轴的交点：(0,1)3(,0)2(2,1)(,1)(,0)22正弦函数、余弦函数的性质先观察区间[0,2π]上的函数图象：在函数的图象上，起关键作用的点有：cos,[0,2]yxx2正弦函数、余弦函数的性质思考：研究一个函数的性质常常从哪几个方面考虑？定义域值域周期性奇偶性单调性最值-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinxyxyO1-1222222222222y=cosx2正弦函数、余弦函数的性质1、正弦函数、余弦函数的图像向左、向右无限伸展；2、正弦函数、余弦函数的图像夹在两平行直线y=1与y=-1之间.即正弦函数、余弦函数由图象易得以下性质：2正弦函数、余弦函数的性质定义域:R,值域:[-1,1]思考：观察上图,正弦曲线每相隔个单位重复出现.其理论依据是什么？-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinxy2当自变量x的值增加2π的整数倍时，函数值重复出现.数学上，用周期性这个概念来定量地刻画这种“周而复始”的变化规律.2正弦函数、余弦函数的性质对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x+T)=f(x),那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.周期函数定义：2正弦函数、余弦函数的性质思考：周期函数的周期是否是唯一的？正弦函数的周期可以是哪些？周期函数的周期可以不止一个.例如2,4,6…以及…都是正弦函数的周期.事实上，任何一个常数都是它的周期.2k(kk0)Z且-2,-4,-62正弦函数、余弦函数的性质最小正周期:如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期.思考：正弦函数有没有最小正周期？如果有，是多少？如果没有，请说明理由.正弦函数存在最小正周期，是2π2正弦函数、余弦函数...