课时3372_3.2.2双曲线的简单几何性质（第一课时）-3.2.2双曲线的几何性质(第1课时)【公众号悦过学习分享】(1).pptVIP免费

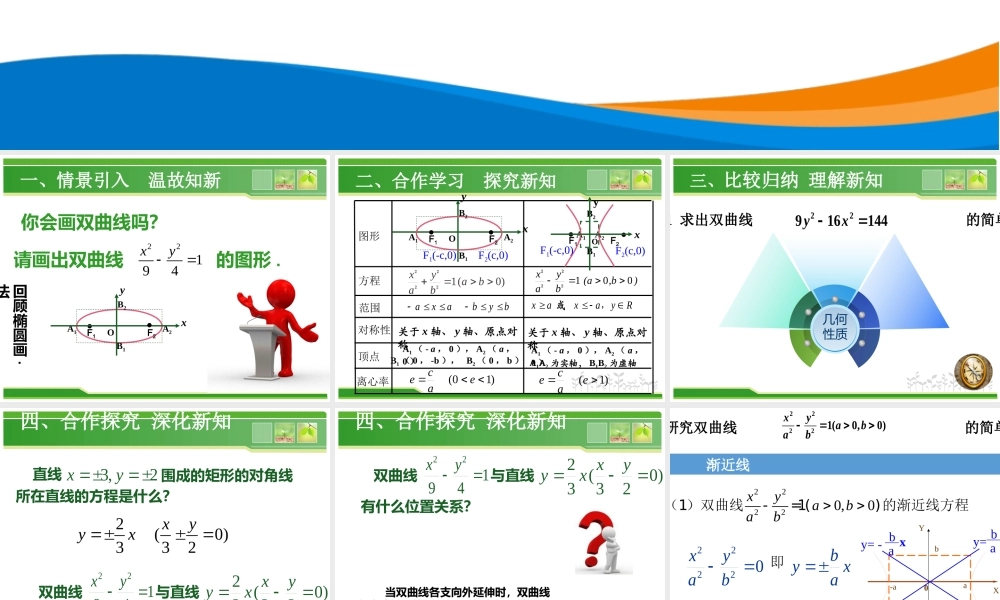
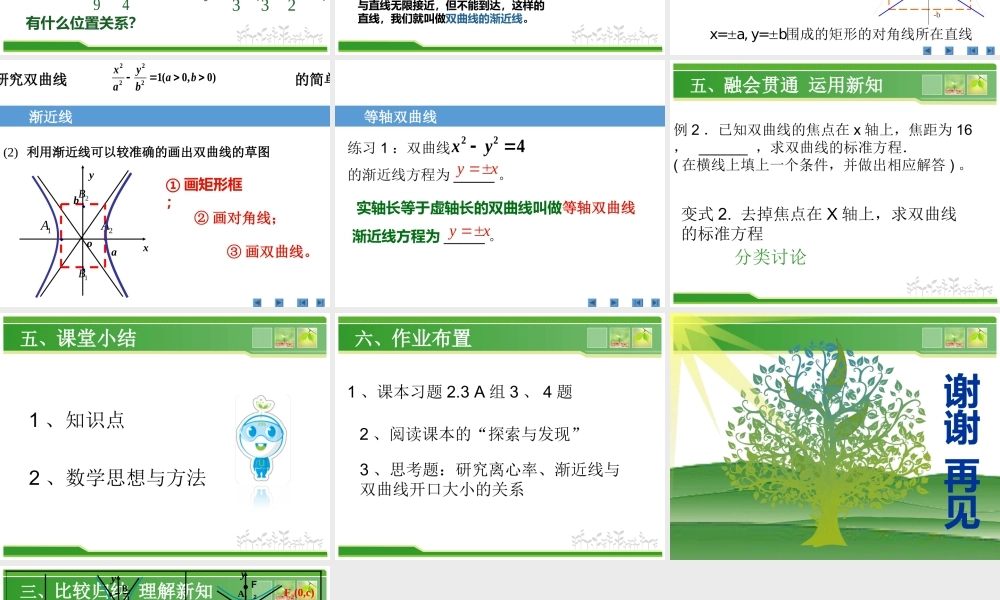
（第一课时）主讲人：育才中学潘红娟3.2.2双曲线的几何性质一、情景引入温故知新你会画双曲线吗？请画出双曲线的图形.22194xyA2B2A1B1.yxO.F1F2回顾椭圆画·法关于x轴、y轴、原点对称图形方程范围对称性顶点离心率yxOA2B2A1B1..F1F2B2A1A2B1bybaxaA1（-a，0），A2（a，0）B1（0，-b），B2（0，b）)10(eaceF1(-c,0)F2(c,0)Oy..xF2F1F1(-c,0)F2(c,0)Ryaxax，或关于x轴、y轴、原点对称A1（-a，0），A2（a，0）A1A2为实轴，B1B2为虚轴)1(eace)0(1babyax2222),b(abyax0012222二、合作学习探究新知三、比较归纳理解新知几何性质1求出双曲线的简单22916144yx四、合作探究深化新知直线3,2xy围成的矩形的对角线所在直线的方程是什么？23yx(0)32xy双曲线22194xy与直线23yx(0)32xy有什么位置关系？当双曲线各支向外延伸时，双曲线与直线无限接近，但不能到达，这样的直线，我们就叫做双曲线的渐近线。四、合作探究深化新知双曲线22194xy与直线23yx(0)32xy有什么位置关系？渐近线研究双曲线的简单22221(0,0)xyabab22220,0xyabab（1）双曲线-=1()的渐近线方程byxax=a,y=b围成的矩形的对角线所在直线YX-aa-bb0y=aby=-abx22220xyab即渐近线研究双曲线的简单22221(0,0)xyabab利用渐近线可以较准确的画出双曲线的草图(2)1A2A1B2Bxyoab①画矩形框；②画对角线；③画双曲线。等轴双曲线练习1：双曲线的渐近线方程为_____。224xyyx实轴长等于虚轴长的双曲线叫做等轴双曲线渐近线方程为_____。yx五、融会贯通运用新知例2．已知双曲线的焦点在x轴上，焦距为16，______，求双曲线的标准方程．(在横线上填上一个条件，并做出相应解答)。变式2.去掉焦点在X轴上，求双曲线的标准方程分类讨论五、课堂小结2、数学思想与方法1、知识点六、作业布置2、阅读课本的“探索与发现”1、课本习题2.3A组3、4题3、思考题：研究离心率、渐近线与双曲线开口大小的关系谢谢再见三、比较归纳理解新知关于x轴、y轴、原点对称图形方程范围对称性顶点离心率1(0)xyabab2222A1（-a，0），A2（a，0）A1（0，-a），A2（0，a）100yx(a,b)ab2222≥≤yayaxR，或关于x轴、y轴、原点对称(1)ceea渐进线ayxb..yB2A1A2B1xOF2F1xB1yO.F2F1B2A1A2.F1(-c,0)F2(c,0)F2(0,c)F1(0,-c)≥≤xaxayR，或(1)ceeabyxa