课时3344_2.1.1倾斜角与斜率（第二课时）-2.1.1倾斜角与斜率（第二课时）【公众号悦过学习分享】(1).pptVIP免费

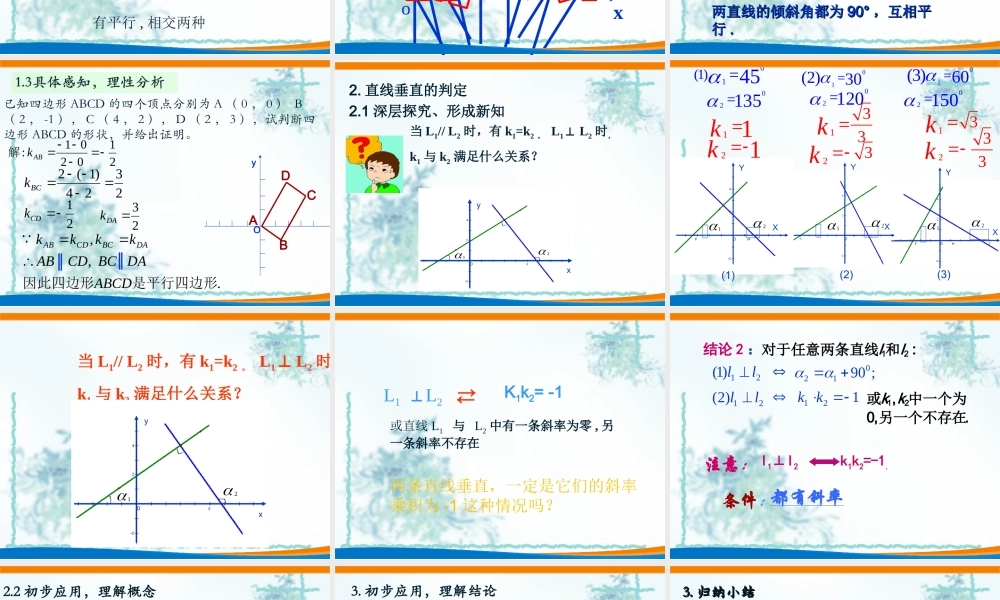
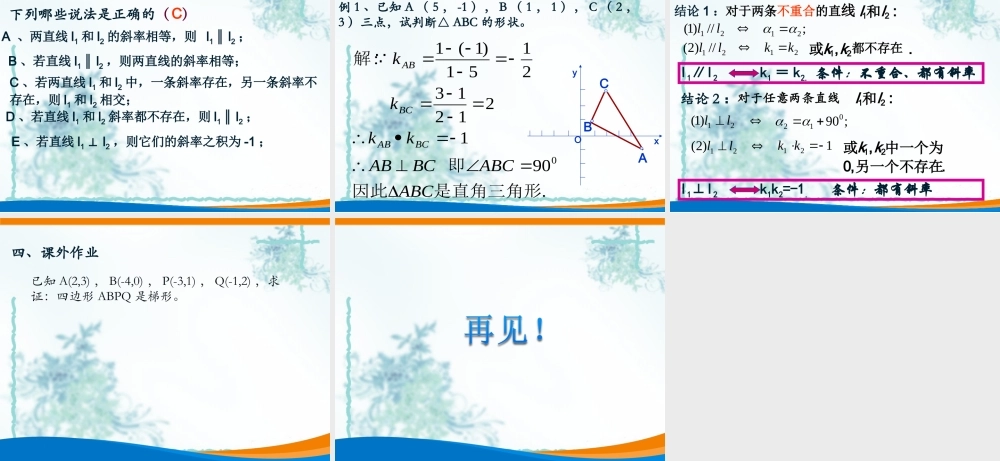
（第二课时）主讲人：坪山高级中学张军2.1.1直线的倾斜角与斜率的直线斜率公式经过)y,x(P,)y,x(P222111)(211212xxxxyyk倾斜角：斜率：在平面直角坐标系中在平面直角坐标系中,,当直线当直线ll与与xx轴相交时，轴相交时，取取xx轴作为基准，轴作为基准，x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.倾斜角不是900的直线，它的倾斜角的正切值叫做这条直线的斜率，常用k来表示.k=tanα1.直线平行的判定1.1复习巩固、引发思考问题1.已知A（2，3），B（-4，0），P（-3，1），Q（-1，2），试判断直线AB与PQ的位置关系，并证明你的结论。OxyABPQ问题2如果两条直线互相平行，它们的倾斜角满足什么关系oxy有平行,相交两种平面上两条直线位置关系oxyL1L2L1L2L1L2L1L2L1L2如果两条直线互相平行，它们的倾斜角满足什么关系？它们的斜率呢？1.2探究新知，形成结论21//)1(ll;21:21ll和结论1：对于两条不重合的直线21//)2(ll21kk.,21都不存在或kkl1∥l2k1＝k2.条件：注意：不重合、都有斜率特殊情况下的两直线平行特殊情况下的两直线平行::两直线的倾斜角都为两直线的倾斜角都为90°90°，互相平，互相平行行..已知四边形ABCD的四个顶点分别为A（0，0）B（2，-1），C（4，2），D（2，3），试判断四边形ABCD的形状，并给出证明。OyDCAB.,,是平行四边形因此四边形ABCDBCDACDABkkkkDABCCDAB∥∥210201:ABk解21CDk2324)1(2BCk23DAk当L1//L2时，有k1=k2。L1⊥L2时，k1与k2满足什么关系？yx122.1深层探究、形成新知2.直线垂直的判定(3)YX12(2)YX12(1)YX1201(1)450213501(2)300212001(3)600215011k21k133k23k13k233k当L1//L2时，有k1=k2。L1⊥L2时k1与k2满足什么关系？yx12L1⊥L2→K1k2=-1或直线L1与L2中有一条斜率为零,另一条斜率不存在←两条直线垂直，一定是它们的斜率乘积为-1这种情况吗？结论2：:21ll和对于任意两条直线21)1(ll;9001221)2(ll121kk.,0,21另一个不存在中一个为或kkl1⊥l2k1k2=-1.条件：注意：都有斜率2.2初步应用，理解概念下列哪些说法是正确的（）CA、两直线l1和l2的斜率相等，则l1l∥2；B、若直线l1l∥2，则两直线的斜率相等；C、若两直线l1和l2中，一条斜率存在，另一条斜率不存在，则l1和l2相交；D、若直线l1和l2斜率都不存在，则l1l∥2；E、若直线l1l⊥2，则它们的斜率之积为-1；例1...