课时3343_2.1.1倾斜角与斜率（第一课时）-2.1.1倾斜角与斜率（第一课时）【公众号悦过学习分享】(1).pptxVIP免费

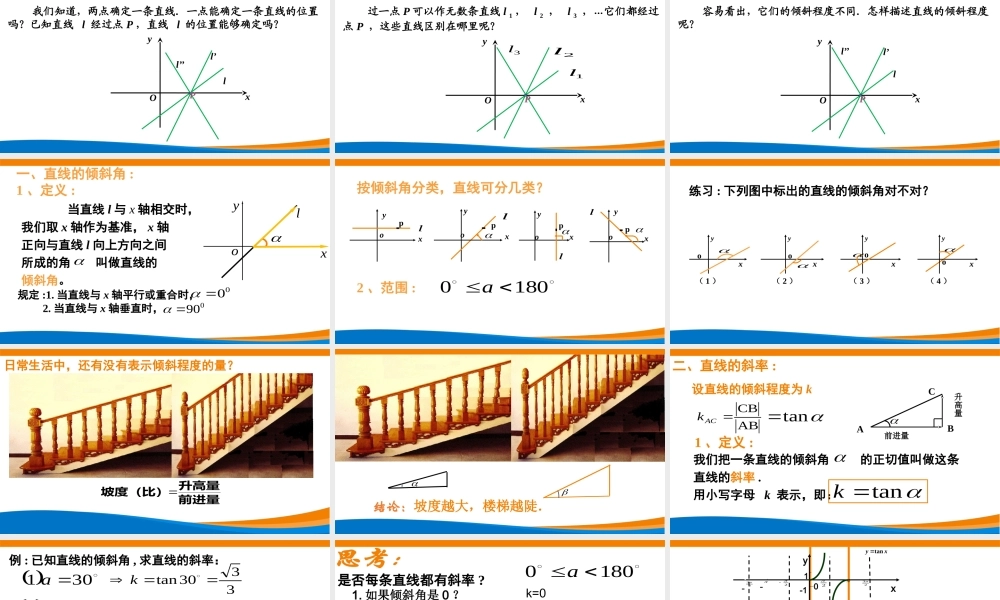
（第一课时）主讲人：深圳市坪山高级中学张忠会深圳市新课程新教材高中数学在线教学3.3.1倾斜角与斜率我们知道，两点确定一条直线．一点能确定一条直线的位置吗？已知直线l经过点P，直线l的位置能够确定吗？问题引入xyOll’l’’P过一点P可以作无数条直线l1，l2，l3，…它们都经过点P，这些直线区别在哪里呢？问题引入xyOP1l1l1l2l3l容易看出，它们的倾斜程度不同．怎样描述直线的倾斜程度呢？问题引入xyOll’l’’Pyolx一、直线的倾斜角:1、定义:当直线l与x轴相交时，我们取x轴作为基准，x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角。规定:1.当直线与x轴平行或重合时，2.当直线与x轴垂直时，00090poyxlypoxlpoyxlpoyxl按倾斜角分类，直线可分几类？2、范围:1800aoxyoxyoxyoxy（1）（2）（3）（4）练习:下列图中标出的直线的倾斜角对不对？前进量升高量坡度（比）日常生活中，还有没有表示倾斜程度的量？结论：坡度越大，楼梯越陡．升高量前进量ABC设直线的倾斜程度为kABCBACktan二、直线的斜率:1、定义:我们把一条直线的倾斜角的正切值叫做这条直线的斜率.用小写字母k表示，即：tank例:已知直线的倾斜角,求直线的斜率：301a3330tank452a145tank603a360tank1505a1204atan1203k3tan1503k是否每条直线都有斜率?3.如果倾斜角是锐角?tan0k2.如果倾斜角是直角?4.如果倾斜角是钝角?tan0k不存在k且角越大k越大且角越大k越大1.如果倾斜角是0？k=01800a练习:关于直线的倾斜角和斜率，其中＿＿＿＿说法是正确的.A.任一条直线都有倾斜角，也都有斜率；B.直线的倾斜角越大，它的斜率就越大；C.平行于x轴的直线的倾斜角是0或π；D.两直线的斜率相等，它们的倾斜角相等E.直线斜率的范围是(－∞，＋∞)..F.一定点和一倾斜角可以唯一确定一条直线DEFx1-1y02223-23-xytan能不能构造一个直角三角形去求？tank由两点确定的直线的斜率:),(111yxP),(222yxP21PPQ当α为锐角时，xyo1x2x1y2y),(12yxQ中在QPPRt12QPQPQPPk1212tantan1212xxyy0倾斜角是锐角时),(12yxQxyo),(111yxP),(222yxP当α为钝角时，180,tan)180tan(tan中在12QPPRtQPQP12tan2112xxyy12122112tanxxyyxxyyk0...