课时4_第六章平面向量及其应用_6.2.3向量的数乘运算 一 【至例6】-课件【公众号悦过学习分享】.pptxVIP免费

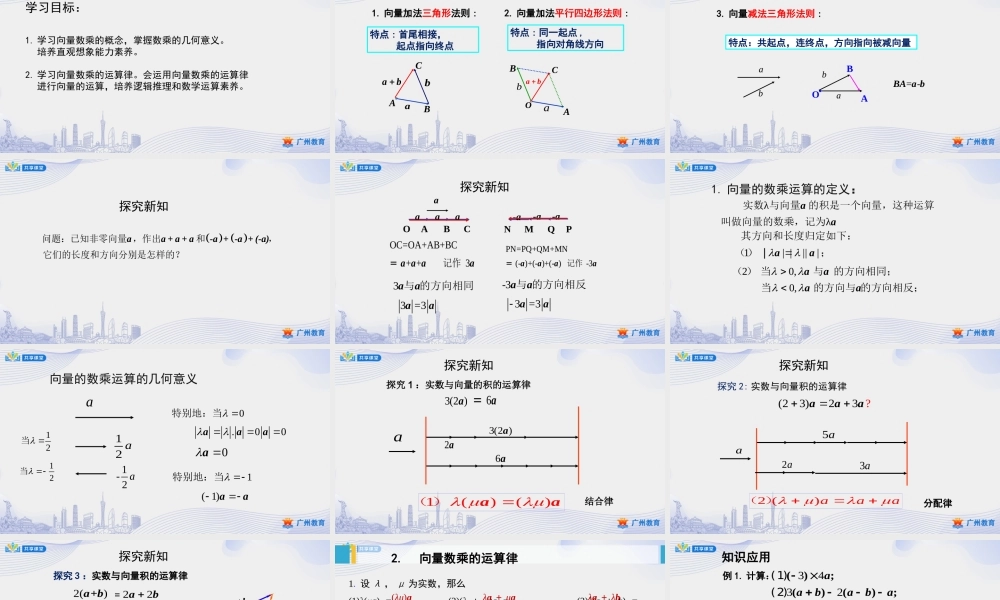
高一人教A版数学必修第二册第六章6.2.3向量的数乘运算广州市番禺区象贤中学苏文丽学习目标：1.学习向量数乘的概念，掌握数乘的几何意义。培养直观想象能力素养。2.学习向量数乘的运算律。会运用向量数乘的运算律进行向量的运算，培养逻辑推理和数学运算素养。1.向量加法三角形法则:aABbCabaAbBOCab特点:首尾相接，起点指向终点特点:同一起点,指向对角线方向2.向量加法平行四边形法则:复习回顾特点：共起点，连终点，方向指向被减向量AO3.向量减法三角形法则:abBab=-�BAab复习回顾问题：已知非零向量，作出和，它们的长度和方向分别是怎样的？aa+a+a-a+-a+(-a)探究新知aaaABCOOC=OA+AB+BC++3aaaa�记作=PN=PQ+QM+MN(-)+(-)+(-)-3aaaa�记作=-a-a-aPQMN33=3与的方向相同aaaa-33=3aaaa与的方向相反-a探究新知1.向量的数乘运算的定义：20,0,（）当与的方向相同；当的方向与的方向相反；aaaaλλ实数与向量的积是一个向量，这种运算叫做向量的数乘，记为aa1|||||其方向和长度归定如下：（）|；aaa12a1-2a0特别地：当12当向量的数乘运算的几何意义12当0a.00aaa1特别地：当(1)aaa2a6a3(2)a3(2)a6a=1()()（）aa探究1：实数与向量的积的运算律探究新知结合律a5a2a3a2()aaa（）?(23)23aaa探究2:实数与向量积的运算律探究新知分配律22ab(3)abab（）探究3：实数与向量积的运算律2a2bab+ab22+ab+ab+ab2()+ab=探究新知分配律2.向量数乘的运算律1.设λ，μ为实数，那么(1)λ(μa)＝_____.(2)(λ＋μ)a＝___________.(3)λ(a＋b)＝________.特别地，(－λ)a＝－(λa)＝_______，λ(a－b)＝_________.2.向量的线性运算向量的、、统称为向量的线性运算，对于任意向量a，b，以及任意实数λ，μ1，μ2，恒有λ(μ1a±μ2b)＝(λμ)aλa＋μaλa＋λbλ(－a)λa－λb加法减法数乘λμ1a±λμ2b例1.计算：34322332();()();()().(1)(2)(3)bbbcbcaaaaaa13412()()aa原式233225()ababab原式解:3233252()abcabcabc原式知识应用例题反思：在数与向量的乘积中去括号、移项、合并同类项、提取公因式等变形手段是适用，但是这里的“同类项”“公因式”是指向量，实数看作是向量的系数.ABCMabD111222�MCACab1111()2222�MDMBDBabab1111()2222�...