课时12_第六章平面向量及其应用_6.4.1平面几何中的向量方法-课件【公众号悦过学习分享】.pptVIP免费

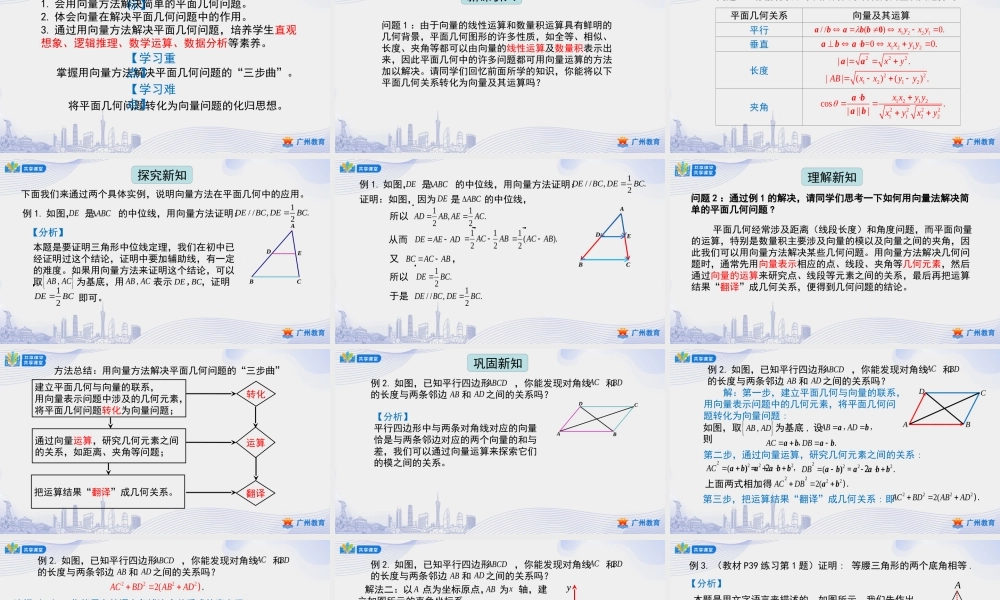
高一年级—人教A版—数学—必修第二册—第六章广州市番禺区实验中学薛兴志6.4.1平面几何中的向量方法【学习目标】1.会用向量方法解决简单的平面几何问题。2.体会向量在解决平面几何问题中的作用。3.通过用向量方法解决平面几何问题，培养学生直观想象、逻辑推理、数学运算、数据分析等素养。掌握用向量方法解决平面几何问题的“三步曲”。将平面几何问题转化为向量问题的化归思想。【学习重点】【学习难点】问题1：由于向量的线性运算和数量积运算具有鲜明的几何背景，平面几何图形的许多性质，如全等、相似、长度、夹角等都可以由向量的线性运算及数量积表示出来，因此平面几何中的许多问题都可用向量运算的方法加以解决。请同学们回忆前面所学的知识，你能将以下平面几何关系转化为向量及其运算吗？新课引入问题1：你能将以下平面几何关系转化为向量及其运算吗？平面几何关系向量及其运算平行垂直长度夹角1221//()0.xyxy0ababb1212=00.xxyyabab222||.xyaa121222221122cos.||||xxyyxyxyabab221212||()().ABxxyy�下面我们来通过两个具体实例，说明向量方法在平面几何中的应用。探究新知【分析】例1.如图，是的中位线，用向量方法证明：ABCDE1//,2DEBCDEBC.EDABC本题是要证明三角形中位线定理，我们在初中已经证明过这个结论，证明中要加辅助线，有一定的难度。如果用向量方法来证明这个结论，可以取为基底，用表示，证明即可。,ABAC�DEBC�，12DEBC�,ABAC�例1.如图，是的中位线，用向量方法证明：ABCDE1//,2DEBCDEBC.EDABC所以11,.22ADABAEAC�从而DEAEAD�又，BCACAB�所以1.2DEBC�于是1//,.2DEBCDEBC证明：如图，因为是的中位线，ABCDE1122ACAB�1().2ACAB�问题2：通过例1的解决，请同学们思考一下如何用向量法解决简单的平面几何问题?理解新知平面几何经常涉及距离（线段长度）和角度问题，而平面向量的运算，特别是数量积主要涉及向量的模以及向量之间的夹角，因此我们可以用向量方法解决某些几何问题。用向量方法解决几何问题时，通常先用向量表示相应的点、线段、夹角等几何元素，然后通过向量的运算来研究点、线段等元素之间的关系，最后再把运算结果“翻译”成几何关系，便得到几何问题的结论。方法总结：用向量方法解决平面几何问题的“三步曲”建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向...