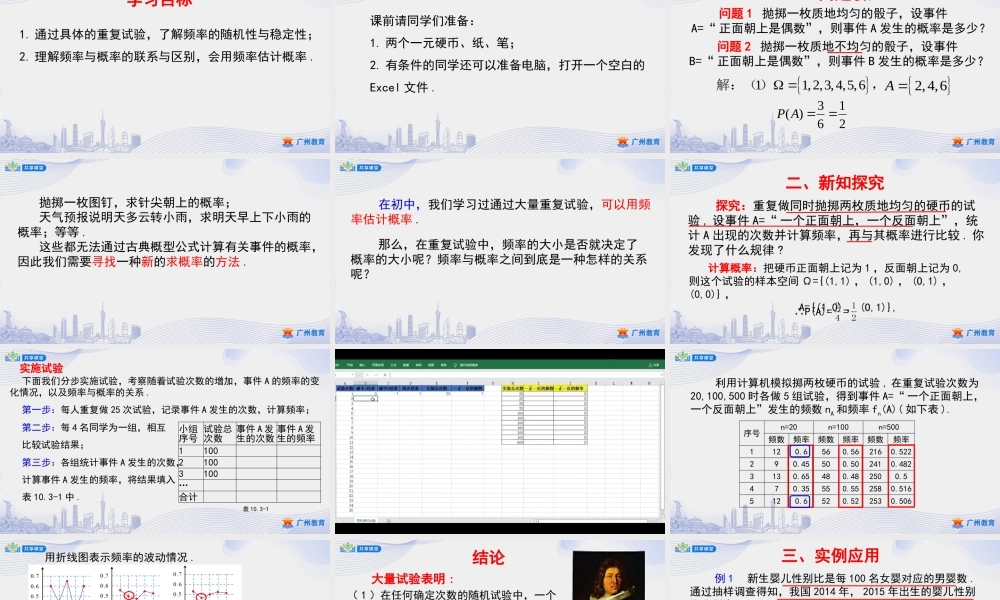
高一—人教A版—数学—必修第二册—第十章广州市花都区狮岭中学田慧10.3.1频率的稳定性学习目标1.通过具体的重复试验,了解频率的随机性与稳定性;2.理解频率与概率的联系与区别,会用频率估计概率.课前请同学们准备:1.两个一元硬币、纸、笔;2.有条件的同学还可以准备电脑,打开一个空白的Excel文件.一、问题引入问题1抛掷一枚质地均匀的骰子,设事件A=“正面朝上是偶数”,则事件A发生的概率是多少?问题2抛掷一枚质地不均匀的骰子,设事件B=“正面朝上是偶数”,则事件B发生的概率是多少?11,2,3,4,5,6解:(),2163)(AP2,4,6A抛掷一枚图钉,求针尖朝上的概率;天气预报说明天多云转小雨,求明天早上下小雨的概率;等等.这些都无法通过古典概型公式计算有关事件的概率,因此我们需要寻找一种新的求概率的方法.在初中,我们学习过通过大量重复试验,可以用频率估计概率.那么,在重复试验中,频率的大小是否就决定了概率的大小呢?频率与概率之间到底是一种怎样的关系呢?二、新知探究探究:重复做同时抛掷两枚质地均匀的硬币的试验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较.你发现了什么规律?计算概率:把硬币正面朝上记为1,反面朝上记为0,则这个试验的样本空间Ω={(1,1),(1,0),(O,1),(0,0)},A={(1,0),(O,1)},∴P(A)==4221下面我们分步实施试验,考察随着试验次数的增加,事件A的频率的变化情况,以及频率与概率的关系.第一步:每人重复做25次试验,记录事件A发生的次数,计算频率;第二步:每4名同学为一组,相互比较试验结果;第三步:各组统计事件A发生的次数,计算事件A发生的频率,将结果填入表10.3-1中.小组序号试验总次数事件A发生的次数事件A发生的频率110021003100…合计实施试验表10.3-1利用计算机模拟掷两枚硬币的试验,在重复试验次数为20,100,500时各做5组试验,得到事件A=“一个正面朝上,一个反面朝上”发生的频数nA和频率fn(A)(如下表).序号n=20n=100n=500频数频率频数频率频数频率1120.6560.562160.522290.45500.502410.4823130.65480.482500.5470.35550.552580.5165120.6520.522530.506用折线图表示频率的波动情况.我们发现:(1)试验次数n相同,频率fn(A)可能不同,这说明随机事件发生的频率具有随机性.(2)从整体来看,频率在概率0.5附近波动.当试验次数较少时,波动幅度较大;当试验次数较大时,波动幅度较小,但试验次数多的波动幅度并不全...