课时16_第三章_3.1.1 函数的概念（2）-课件【公众号悦过学习分享】.pptxVIP免费

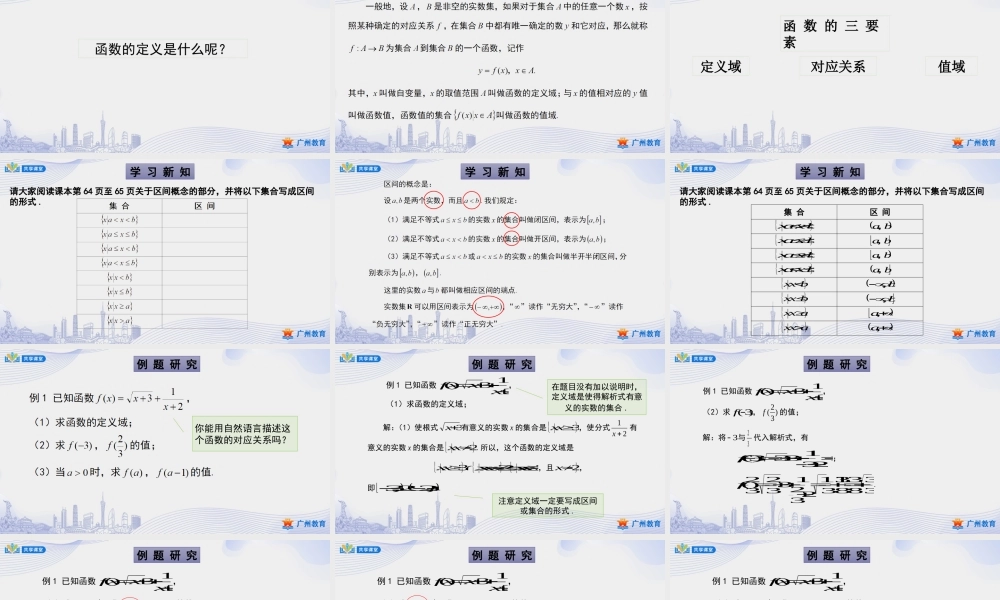
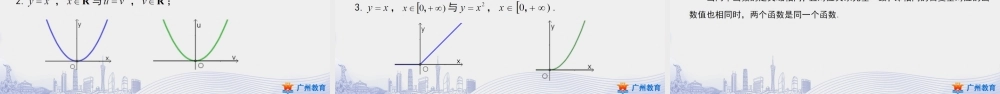高一—人教A版—数学—第三章广州市第五中学张智慧3.1.1函数的概念（2）复习概念函数的定义是什么呢？复习概念复习概念对应关系值域定义域函数的三要素学习新知请大家阅读课本第64页至65页关于区间概念的部分，并将以下集合写成区间的形式.学习新知学习新知请大家阅读课本第64页至65页关于区间概念的部分，并将以下集合写成区间的形式.集合区间bxaxba，bxaxba，bxaxba，bxaxba，bxxb，bxxb，axx，aaxx，a例题研究你能用自然语言描述这个函数的对应关系吗？例题研究注意定义域一定要写成区间或集合的形式.在题目没有加以说明时，定义域是使得解析式有意义的实数的集合.例1已知函数213)(xxxf，（1）求函数的定义域；解：（1）使根式3x有意义的实数x的集合是3xx，使分式21x有意义的实数x的集合是2xx.所以，这个函数的定义域是3xx32xxxx，且2x，即，，223.例题研究例1已知函数213)(xxxf，（2）求)3(f，)32(f的值；解：将3与32代入解析式，有123133)3(f；33383833112321332)32(f.例题研究例1已知函数213)(xxxf，（3）当0a时，求)(af，)1(af的值.例题研究例1已知函数213)(xxxf，（3）当0a时，求)(af，)1(af的值.这个条件的作用是什么呢？例题研究例1已知函数213)(xxxf，（3）当0a时，求)(af，)1(af的值.解：因为0a，所以)1()(afaf，有意义.213)(aaaf；11221131)1(aaaaaf.课堂思考31a，且21a，即2a，且1a.思考1已知函数213)(xxxf，若)1(af有意义，如何求实数a的取值范围呢？课堂练习1.已知函数xxxf23)(3，（1）求)2(f，)2(f，)2()2(ff的值；（2）求)(af，)(af，)()(afaf的值.课堂练习解：（1）将2，2代入解析式，有282223)2(3f；282223)2(3）（）（f；0)2()2(ff.（2）将a，a代入解析式，有aaaf23)(2；aaaaaf23)(2)(3)(22；02323)()(33aaaaafaf.课堂练习函数xxxf23)(3，满足：Ra，0)()(afaf.课堂思考课堂思考课堂思考课堂思考课堂思考课堂思考答：不一定.例如函数2xy，Rx与2xy，...