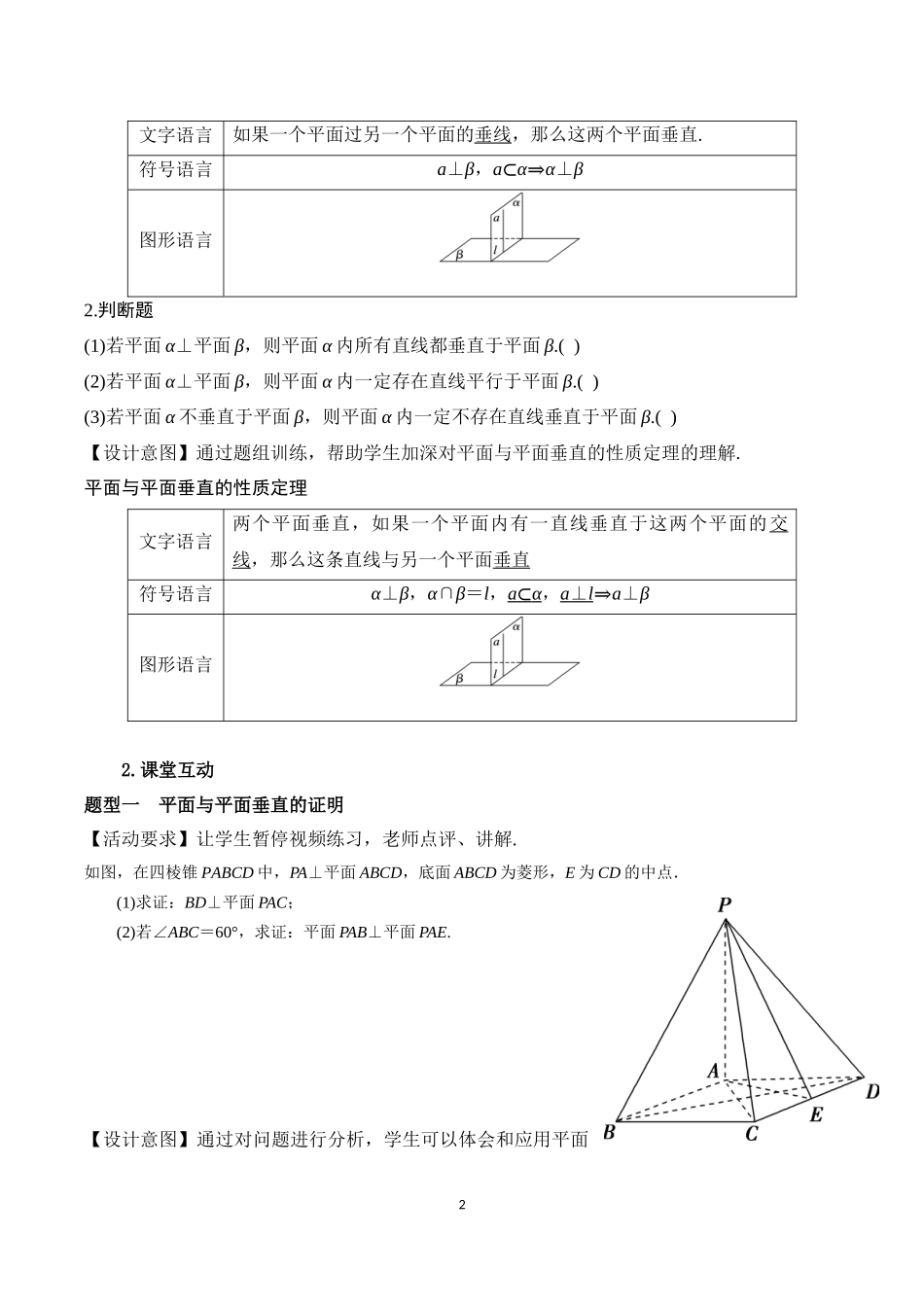
17.4空间中的垂直关系(面面垂直判定、性质)(人教A版普通高中教科书数学必修第二册第八章)深圳第二外国语学校刘娜一、教学目标1.进一步加深理解和掌握平面与平面垂直的定义、判定定理及性质定理,并能应用定理解决相关问题;2.理顺空间垂直位置关系的知识架构,并能应用相关知识对问题进行分析、转化和解决;3.通过平面与平面垂直判定和性质定理的综合应用,以及空间问题平面化的思维方式,体会化归思想方法的应用.二、教学重难点1.平面与平面垂直的判定定理和性质定理的应用.2.应用定理证明过程中表述的条理性和严谨性.三、教学过程1.知识梳理1.1面面垂直的定义(1)定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.平面α与平面β垂直,记作:α⊥β.(2)画法:如图,画两个互相垂直的平面时,通常把表示平面的两个平行四边形的一组边画成垂直.【设计意图】复习面面垂直的定义,做到温故而知新.1.2【微训练】1.对于直线m,n和平面α,β,能得出α⊥β的一个条件是()A.m⊥n,m∥α,n∥βB.m⊥n,α∩β=m,n⊂αC.m∥n,n⊥β,m⊂αD.m∥n,m⊥α,n⊥β【设计意图】通过小题训练,帮助学生回顾平面与平面垂直的判定定理.平面与平面垂直的判定定理2文字语言如果一个平面过另一个平面的垂线,那么这两个平面垂直.符号语言a⊥β,a⊂α⇒α⊥β图形语言2.判断题(1)若平面α⊥平面β,则平面α内所有直线都垂直于平面β.()(2)若平面α⊥平面β,则平面α内一定存在直线平行于平面β.()(3)若平面α不垂直于平面β,则平面α内一定不存在直线垂直于平面β.()【设计意图】通过题组训练,帮助学生加深对平面与平面垂直的性质定理的理解.平面与平面垂直的性质定理文字语言两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直符号语言α⊥β,α∩β=l,a⊂α,a⊥l⇒a⊥β图形语言2.课堂互动题型一平面与平面垂直的证明【活动要求】让学生暂停视频练习,老师点评、讲解.如图,在四棱锥PABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点.(1)求证:BD⊥平面PAC;(2)若∠ABC=60°,求证:平面PAB⊥平面PAE.【设计意图】通过对问题进行分析,学生可以体会和应用平面3与平面垂直的判定定理在分析问题和解决问题中的转化功能,体会应用所学知识解决问题的心理愉悦.老师点评旨在规范学生的解题格式,注重表述的条理性和严谨性.题型二平面与平面垂直的性质及应用【活动要求...