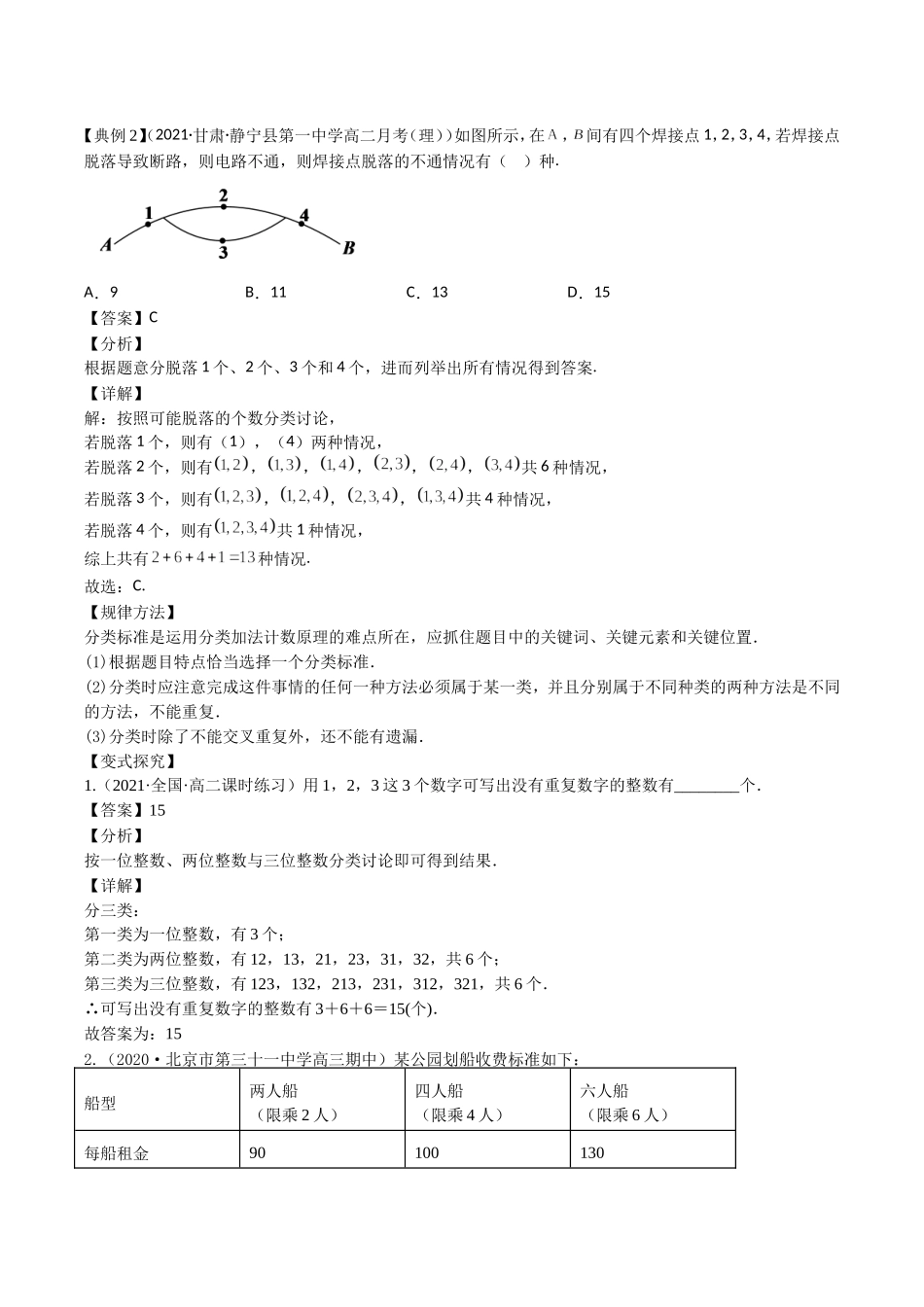
5.3排列组合(两个计数原理)新课程考试要求1.理解分类加法计数原理和分步乘法计数原理,会解决简单的计数问题.核心素养本节涉及数学运算、数学建模、数学抽象等核心数学素养.高考预测(1)考查两个计数原理;(2)考查排列组合问题、概率计算中两个计数原理的应用.(3)两个计数原理是解决排列、组合问题的基本方法,同时又能独立地解决一些简单的计数问题,通常与排列组合问题或概率计算问题综合考查.【知识清单】1.分类加法计数原理(加法原理)的概念一般形式:完成一件事有n类不同方案,在第1类方案中有1m种不同的方法,在第2类方案中有2m种不同的方法,……,在第n类方案中有nm种不同的方法,那么完成这件事共有N=1m+2m+……+nm种不同的方法.2.分步乘法计数原理(乘法原理)的概念一般形式:完成一件事需要n个步骤,做第1步有1m种不同的方法,做第2步有2m种不同的方法,……,做第n步有nm种不同的方法,那么完成这件事共有N=12nmmm…种不同的方法.3.两个原理的区别:(1)“每类”间与“每步”间的关系不同:分类加法计数原理中的每一类方案中的任何一种方法、不同类之间的任何一种方法都是相互独立,互不依赖的,且是一次性的;而分步乘法计数原理中的每一步是相互依赖,且是连续性的.(2)“每类”与“每步”完成的效果不同:分类加法计数原理中所描述的每一种方法完成后,整个事件就完成了,而分步乘法计数原理中每一步中的每一种方法得到的只是中间结果,任何一步都不能独立完成这件事.4.切实理解“完成一件事”的含义,以确定需要分类还是需要分步进行,同时要优先考虑题中的限制条件.【考点分类剖析】考点一:分类加法计数原理【典例1】(2021·江西·横峰中学高二期中(理))由数字1,2,3组成的无重复数字的整数中,偶数的个数为()A.15B.12C.10D.5【答案】D【分析】首先根据题意分成一位偶数,二位偶数和三位偶数三类,再利用分类加法原理求解即可.【详解】分三类,第一类组成一位整数,偶数有2,共1个;第二类组成两位整数,其中偶数有12和32,共2个;第三类组成三位整数,其中偶数有132和312,共2个.由分类加法计数原理知共有偶数5个.故选:D【典例2】(2021·甘肃·静宁县第一中学高二月考(理))如图所示,在,间有四个焊接点1,2,3,4,若焊接点脱落导致断路,则电路不通,则焊接点脱落的不通情况有()种.A.9B.11C.13D.15【答案】C【分析】根据题意分脱落1个、2个、3个和4个,进而列举出所有情况得到答...