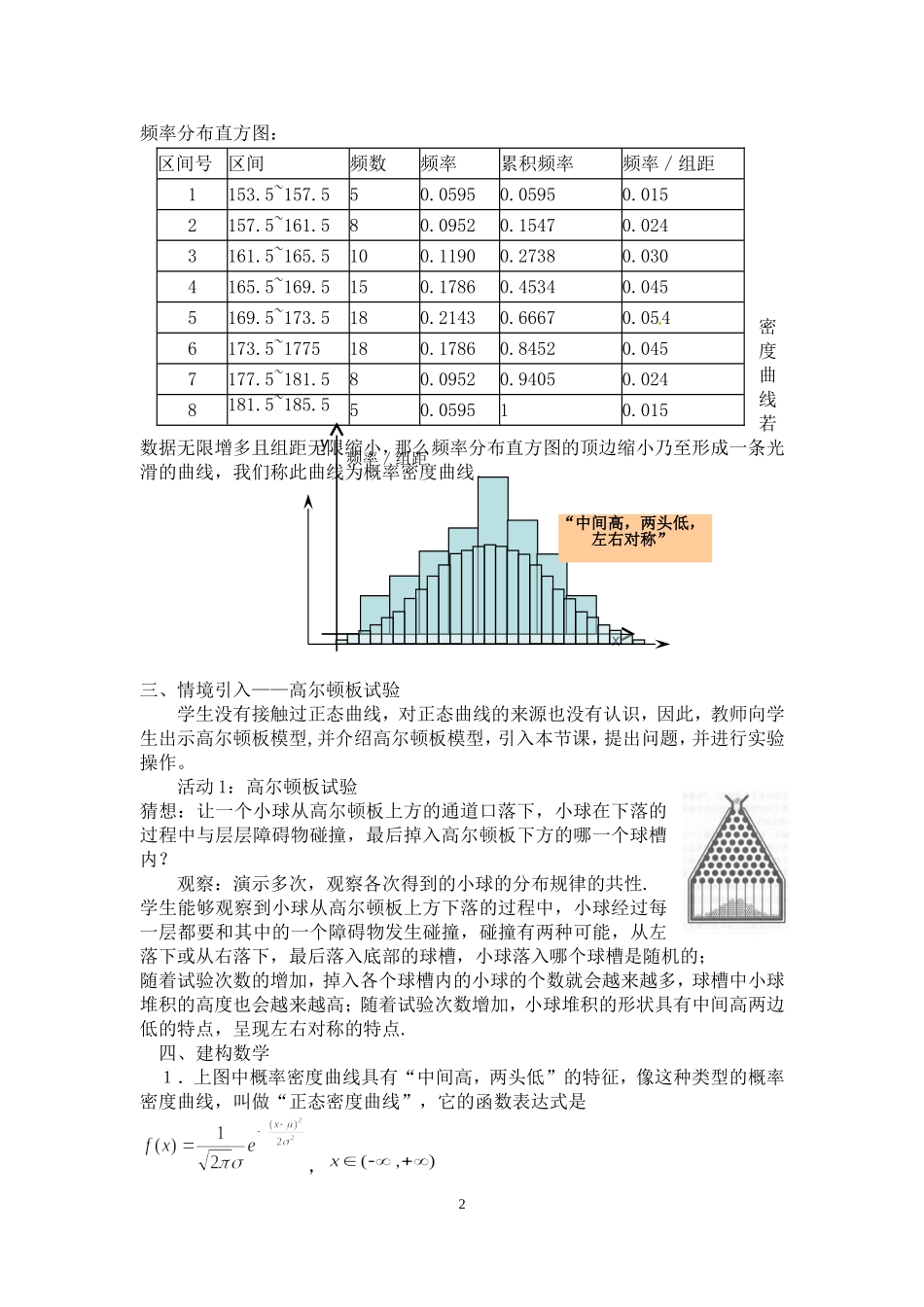
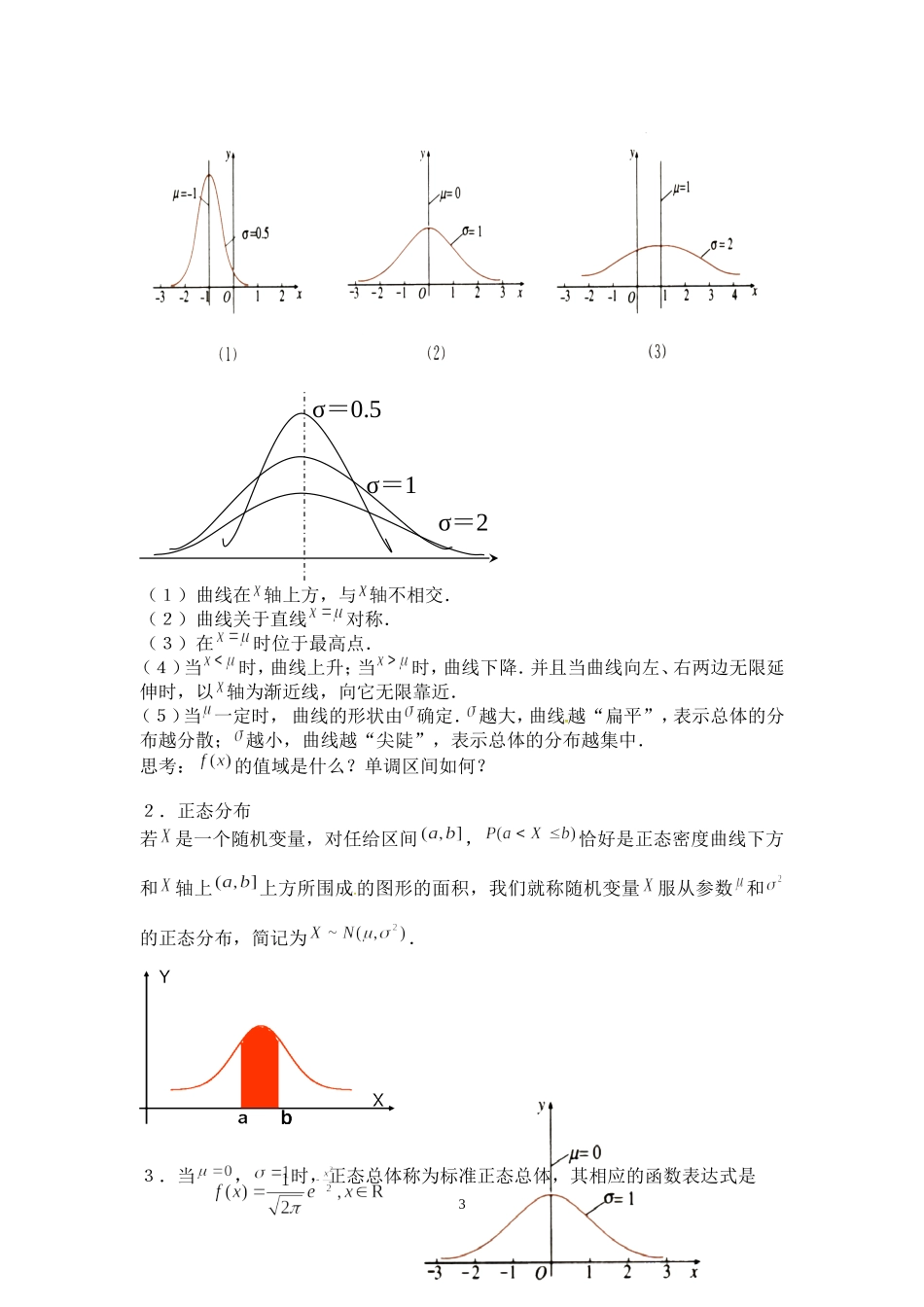
§7.5《正态分布》的教学设计龙岗区东升学校王念珠【教学内容】人教版第三册7.5《正态分布》;【设计依据】学生已经学习了频率分布直方图、离散型随机变量等相关知识,这为本节课学习奠定了基础,而正态分布研究是连续型随机变量,既是对前面内容的补充、拓展。又为学生初步应用正态分布知识解决实际问题提供了理论依据;【教学目标】了解正态分布在实际生活中的意义和作用;掌握正态分布的特点及正态分布曲线所表示的意义、性质;【教学重点】正态分布函数和正态曲线的性质。【教学难点】正态曲线的性质。【教学准备】【教学过程】一、问题情境1.情境引入:从某中学男生中随机抽取84名,测量身高,数据如下(单位:)1641751701631681611771731651811551781641611741771751681701691741641761811811671781681691591741671711761721741591801541731701711741721711851641721631671681701741721691821671651721711851571741641681731661721611781621721791611601751691691751611551561821822.提出问题:上述数据的分布有怎样的特点?二、学生活动通过频率分布直方图来分析数据:首先确定组数,组距.1频率分布直方图:密度曲线若数据无限增多且组距无限缩小,那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线,我们称此曲线为概率密度曲线.三、情境引入——高尔顿板试验学生没有接触过正态曲线,对正态曲线的来源也没有认识,因此,教师向学生出示高尔顿板模型,并介绍高尔顿板模型,引入本节课,提出问题,并进行实验操作。活动1:高尔顿板试验猜想:让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层障碍物碰撞,最后掉入高尔顿板下方的哪一个球槽内?观察:演示多次,观察各次得到的小球的分布规律的共性.学生能够观察到小球从高尔顿板上方下落的过程中,小球经过每一层都要和其中的一个障碍物发生碰撞,碰撞有两种可能,从左落下或从右落下,最后落入底部的球槽,小球落入哪个球槽是随机的;随着试验次数的增加,掉入各个球槽内的小球的个数就会越来越多,球槽中小球堆积的高度也会越来越高;随着试验次数增加,小球堆积的形状具有中间高两边低的特点,呈现左右对称的特点.四、建构数学1.上图中概率密度曲线具有“中间高,两头低”的特征,像这种类型的概率密度曲线,叫做“正态密度曲线”,它的函数表达式是,2区间号区间频数频率累积频率频率/组距1153.5~157.550.05950.05950.0152157.5~161.580.09520.15470.024316...