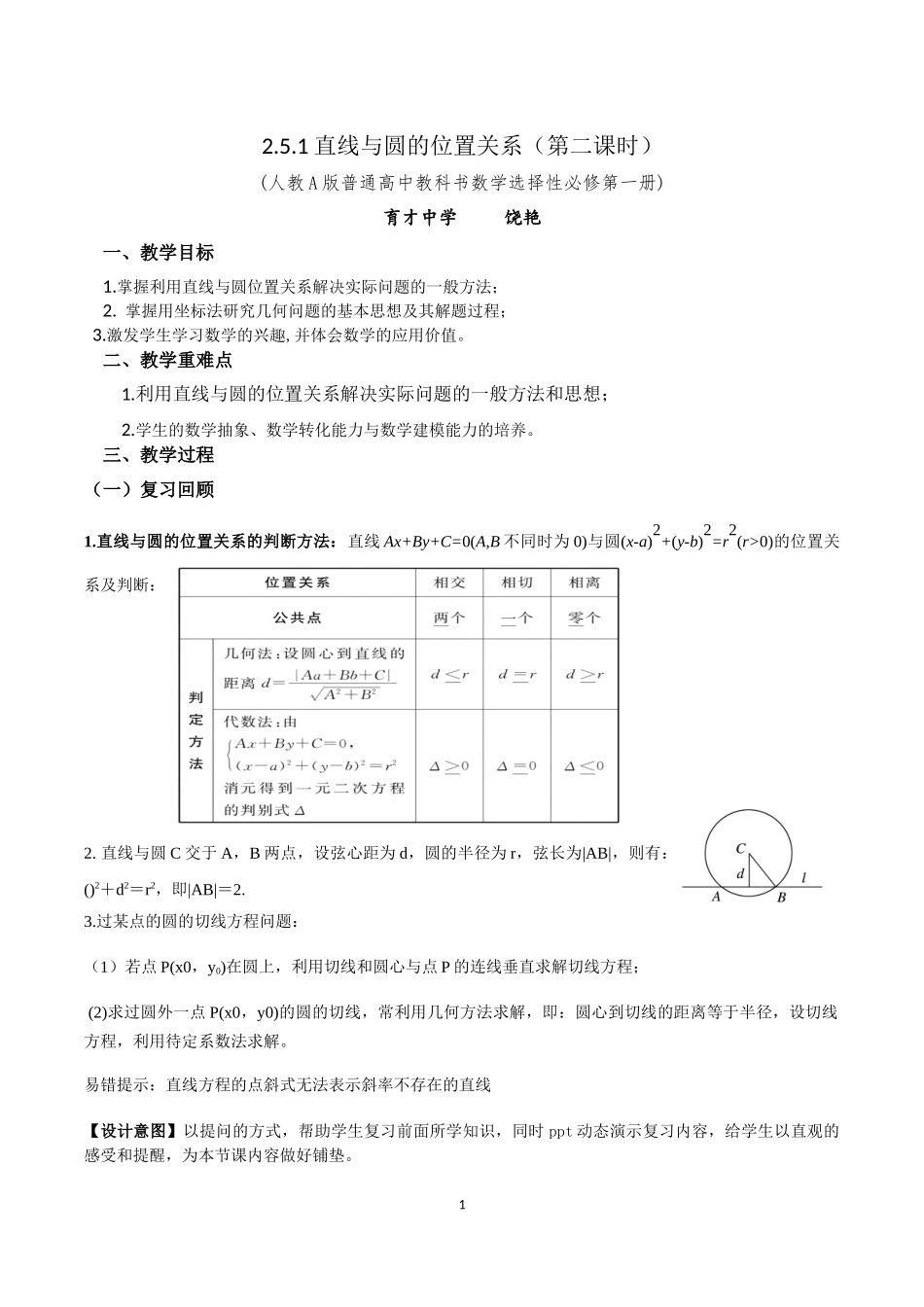
12.5.1直线与圆的位置关系(第二课时)(人教A版普通高中教科书数学选择性必修第一册)育才中学饶艳一、教学目标1.掌握利用直线与圆位置关系解决实际问题的一般方法;2.掌握用坐标法研究几何问题的基本思想及其解题过程;3.激发学生学习数学的兴趣,并体会数学的应用价值。二、教学重难点1.利用直线与圆的位置关系解决实际问题的一般方法和思想;2.学生的数学抽象、数学转化能力与数学建模能力的培养。三、教学过程(一)复习回顾1.直线与圆的位置关系的判断方法:直线Ax+By+C=0(A,B不同时为0)与圆(x-a)2+(y-b)2=r2(r>0)的位置关系及判断:2.直线与圆C交于A,B两点,设弦心距为d,圆的半径为r,弦长为|AB|,则有:()2+d2=r2,即|AB|=2.3.过某点的圆的切线方程问题:(1)若点P(x0,y0)在圆上,利用切线和圆心与点P的连线垂直求解切线方程;(2)求过圆外一点P(x0,y0)的圆的切线,常利用几何方法求解,即:圆心到切线的距离等于半径,设切线方程,利用待定系数法求解。易错提示:直线方程的点斜式无法表示斜率不存在的直线【设计意图】以提问的方式,帮助学生复习前面所学知识,同时ppt动态演示复习内容,给学生以直观的感受和提醒,为本节课内容做好铺垫。2(二)问题引入新课台风中心从A地以20km/h的速度向东北方向移动,离台风中心30km内的地区为危险区,城市B在A地正东40km处,则城市B处于危险区的时间为多少?【设计意图】通过现实生活中的实例,让学生体会到数学源于生活并可以指导生活,感受数学的魅力(三)讲授新课例3.如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m).问题1.如何建立适当的平面直角坐标系?(大家分组讨论,给出方案)(教师展示学生方案,引导学生回忆建立平面直角坐标系应该遵循的原则,选择最合适的坐标系。)学生:(回忆回答建立直角坐标系的原则)①若曲线是轴对称图形,则可选它的对称轴为坐标轴.②常选特殊点作为直角坐标系的原点.③尽量使已知点位于坐标轴上.建立适当的直角坐标系,会简化运算过程.【设计意图】进一步巩固建立适当的坐标系的方法技巧师生活动:选择最适合的坐标系后在平民啊直角坐标系下解决代数问题:预设答案:解:建立如图所示的直角坐标系,使线段AB所在直线为x轴,O为坐标原点,圆心在y轴上,由题意,点P,B的坐标分别为(0,4),(10,0),设圆心坐标是(0,b),圆的半径是r,那么圆的方程是x2+(y-b)2=r2.因为P,B...