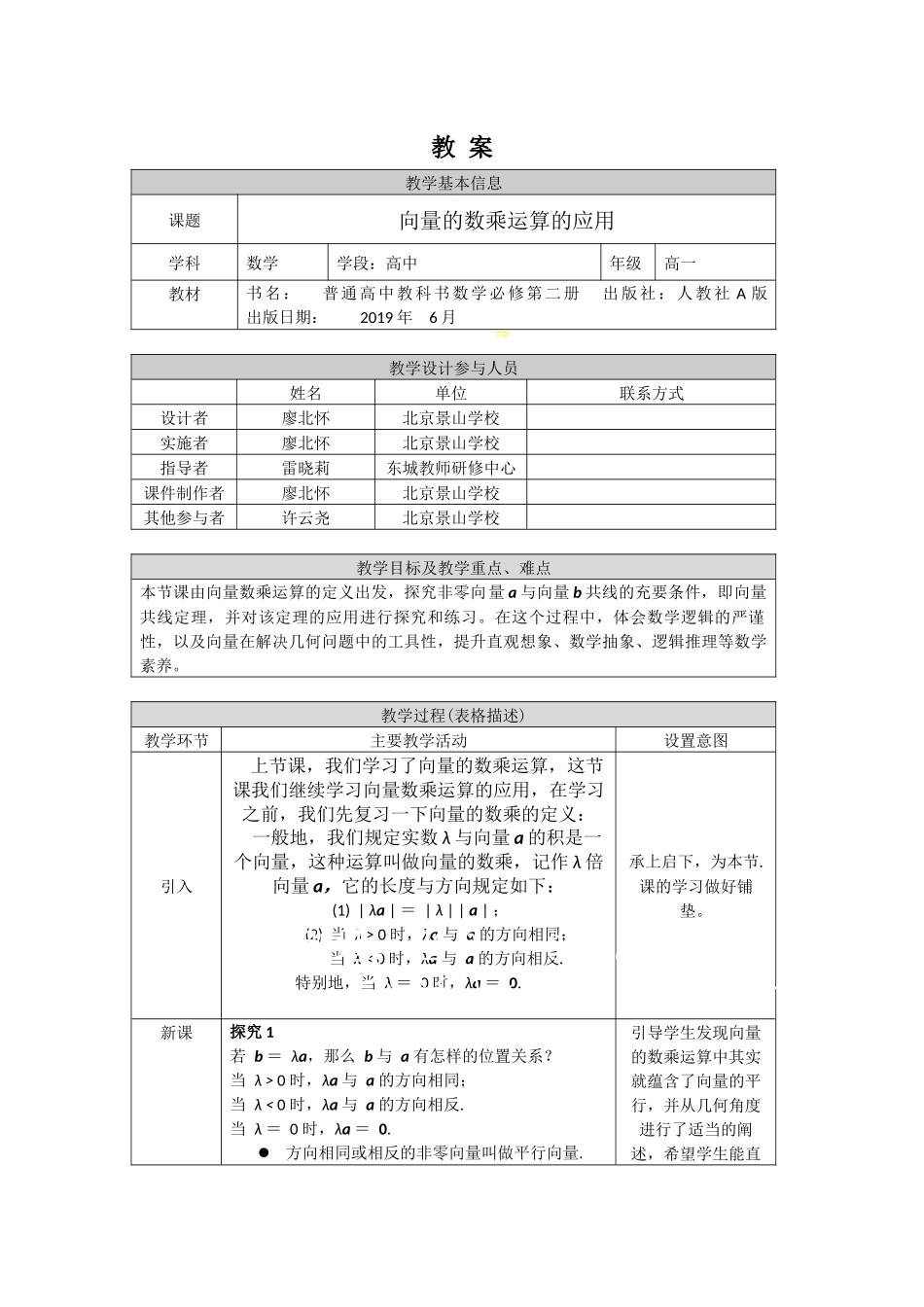
教案教学基本信息课题向量的数乘运算的应用学科数学学段:高中年级高一教材书名:普通高中教科书数学必修第二册出版社:人教社A版出版日期:2019年6月教学设计参与人员姓名单位联系方式设计者廖北怀北京景山学校实施者廖北怀北京景山学校指导者雷晓莉东城教师研修中心课件制作者廖北怀北京景山学校其他参与者许云尧北京景山学校教学目标及教学重点、难点本节课由向量数乘运算的定义出发,探究非零向量a与向量b共线的充要条件,即向量共线定理,并对该定理的应用进行探究和练习。在这个过程中,体会数学逻辑的严谨性,以及向量在解决几何问题中的工具性,提升直观想象、数学抽象、逻辑推理等数学素养。教学过程(表格描述)教学环节主要教学活动设置意图引入上节课,我们学习了向量的数乘运算,这节课我们继续学习向量数乘运算的应用,在学习之前,我们先复习一下向量的数乘的定义:一般地,我们规定实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作λ倍向量a,它的长度与方向规定如下:(1)|λa|=|λ||a|;(2)当λ>0时,λa与a的方向相同;当λ<0时,λa与a的方向相反.特别地,当λ=0时,λa=0.承上启下,为本节.课的学习做好铺垫。新课探究1若b=λa,那么b与a有怎样的位置关系?当λ>0时,λa与a的方向相同;当λ<0时,λa与a的方向相反.当λ=0时,λa=0.方向相同或相反的非零向量叫做平行向量.引导学生发现向量的数乘运算中其实就蕴含了向量的平行,并从几何角度进行了适当的阐述,希望学生能直(2)当λ>0时,λa与a的方向相同当λ<0时,λa与a的方向相反特别地,当λ=0时,λa=0.规定零向量与任意向量平行.平行向量也叫共线向量.结论:b=λab//a.aλa探究2若b//a,是否存在实数λ,使得b=λa?(1)当a≠0,b≠0时,存在唯一一个实数λ,使得b=λa.(2)当a≠0,b=0时,存在唯一一个实数λ,使得b=λa.(3)当a=0,b≠0时,不存在这样的实数λ,使得b=λa.(4)当a=0,b=0时,λ取任意实数,都使得b=λa.结论:所以当b//a,a≠0时,存在唯一一个实数λ,使得b=λa.问题:若存在唯一一个实数λ,使得b=λa能推出b//a,a≠0吗?分析:若a=0,则b=λa=0,此时,λ可以取任意实数,不唯一.定理向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使b=λa.判断:(1)向量a(a≠0)与b共线,则存在实数λ,使得a=λb;()(2)b//a的充要条件是存在不全为零的实数λ和μ,使得λa=μb;()(3)若向量a与b不共线,且λa=μb,则实数λ=μ=0.()...