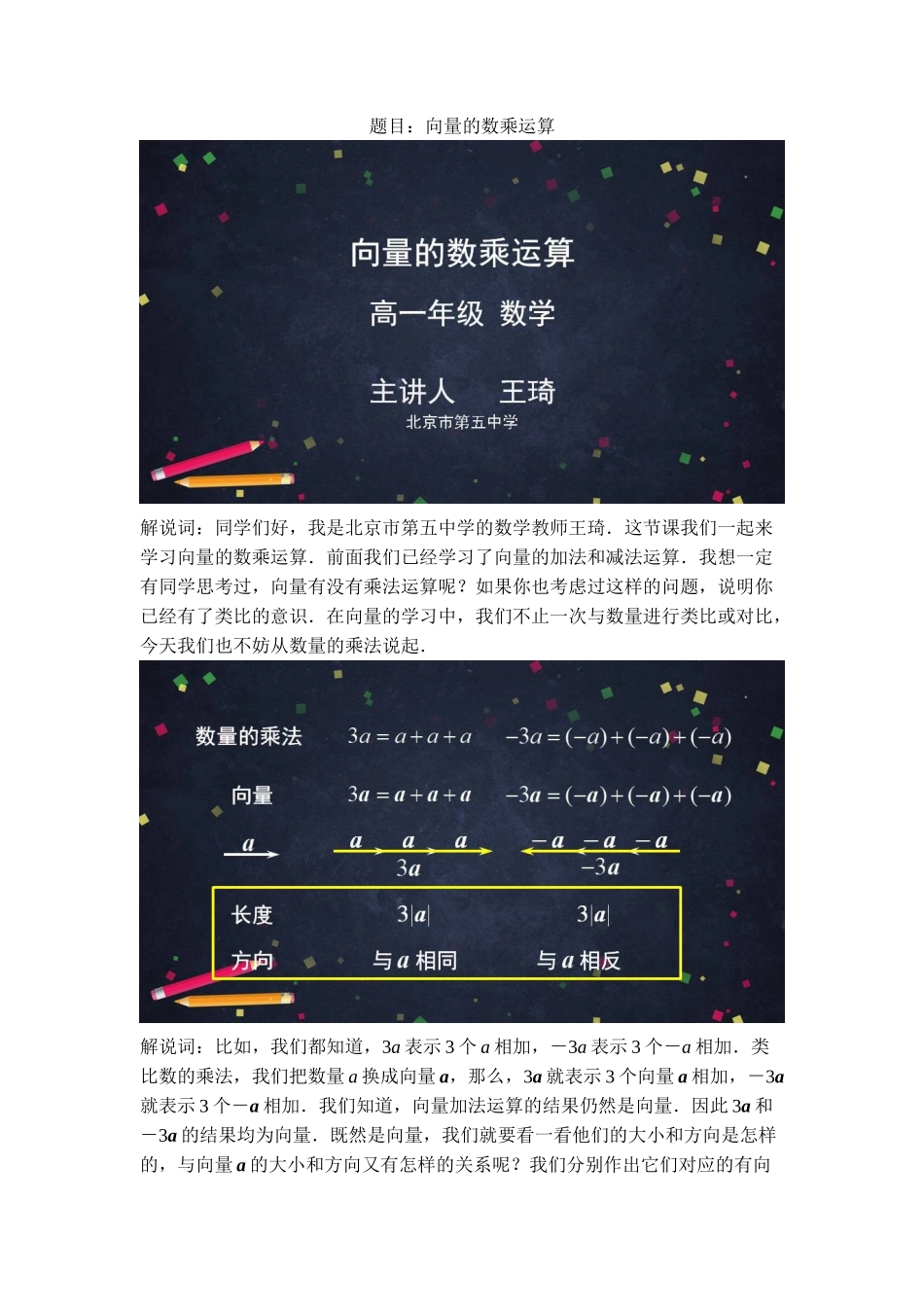
题目:向量的数乘运算解说词:同学们好,我是北京市第五中学的数学教师王琦.这节课我们一起来学习向量的数乘运算.前面我们已经学习了向量的加法和减法运算.我想一定有同学思考过,向量有没有乘法运算呢?如果你也考虑过这样的问题,说明你已经有了类比的意识.在向量的学习中,我们不止一次与数量进行类比或对比,今天我们也不妨从数量的乘法说起.解说词:比如,我们都知道,3a表示3个a相加,-3a表示3个-a相加.类比数的乘法,我们把数量a换成向量a,那么,3a就表示3个向量a相加,-3a就表示3个-a相加.我们知道,向量加法运算的结果仍然是向量.因此3a和-3a的结果均为向量.既然是向量,我们就要看一看他们的大小和方向是怎样的,与向量a的大小和方向又有怎样的关系呢?我们分别作出它们对应的有向线段来看一看,按照向量加法的三角形法则,将三个向量a首尾相接,就得到了3a,同理,我们先做出向量a的相反向量——-a,再将3个-a首尾相接,就得到了-3a.不难发现,3a和-3a,它们的长度都等于,我们可以归纳为用这个实数的绝对值乘以.显然,3a的方向与向量a的方向相同.-3a的方向与向量a的方向相反.更一般地,对于任意实数乘以向量a,我们可以类似地规定结果的长度和方向.解说词:由此,我们给出向量数乘运算的定义.解说词:一般地,我们规定实数λ与向量a的积是一个向量,记作λa,它的长度与方向规定如下:(1);(2)当λ>0时,λa与向量a的方向相同;当λ<0时,λa与向量a的方向相反.由于这种运算是数量与向量相乘,所以我们把它叫做向量的数乘.听到这里,可能有同学会想,向量和向量之间是否可以相乘呢,我们在后续课程中会对此进行讨论.解说词:可能还有同学有疑问,λ>0和λ<0时,对λa的方向都作出了规定,当λ=0时,λa的方向又是怎样的呢?事实上,当λ=0时,,模为0的向量就是零向量,所以0a=0.这说明0与任意向量数乘运算的结果均为零向量.事实上,当向量a=0时,,所以,λ0=0.这说明零向量与任意实数数乘运算的结果均为零向量.这是两种较为特殊的情况.解说词:有了向量数乘运算的定义,我们来做个小练习:已知向量a如图所示,求作向量b=0.5a,向量c=-2a.由定义可知,向量b的长度等于向量a长度的0.5倍,因此我们先作出线段AB,它的长度是向量a长度的0.5倍,因为0.5>0,所以向量b与向量a的方向相同,因此,向量b=.同理,向量c的长度应该等于向量a长度的2倍,所以我们作出线段CD,它的长度为向量a长...