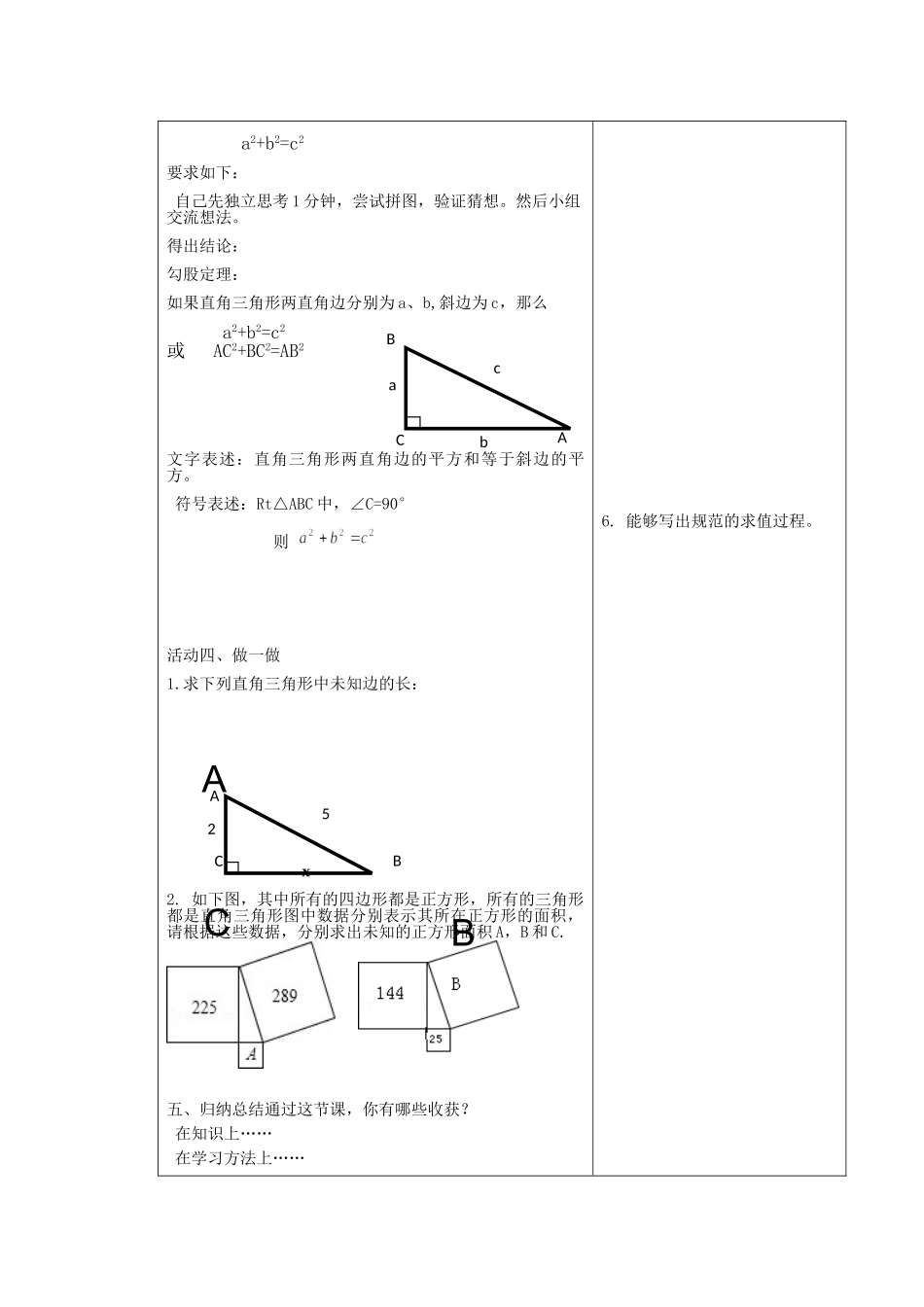
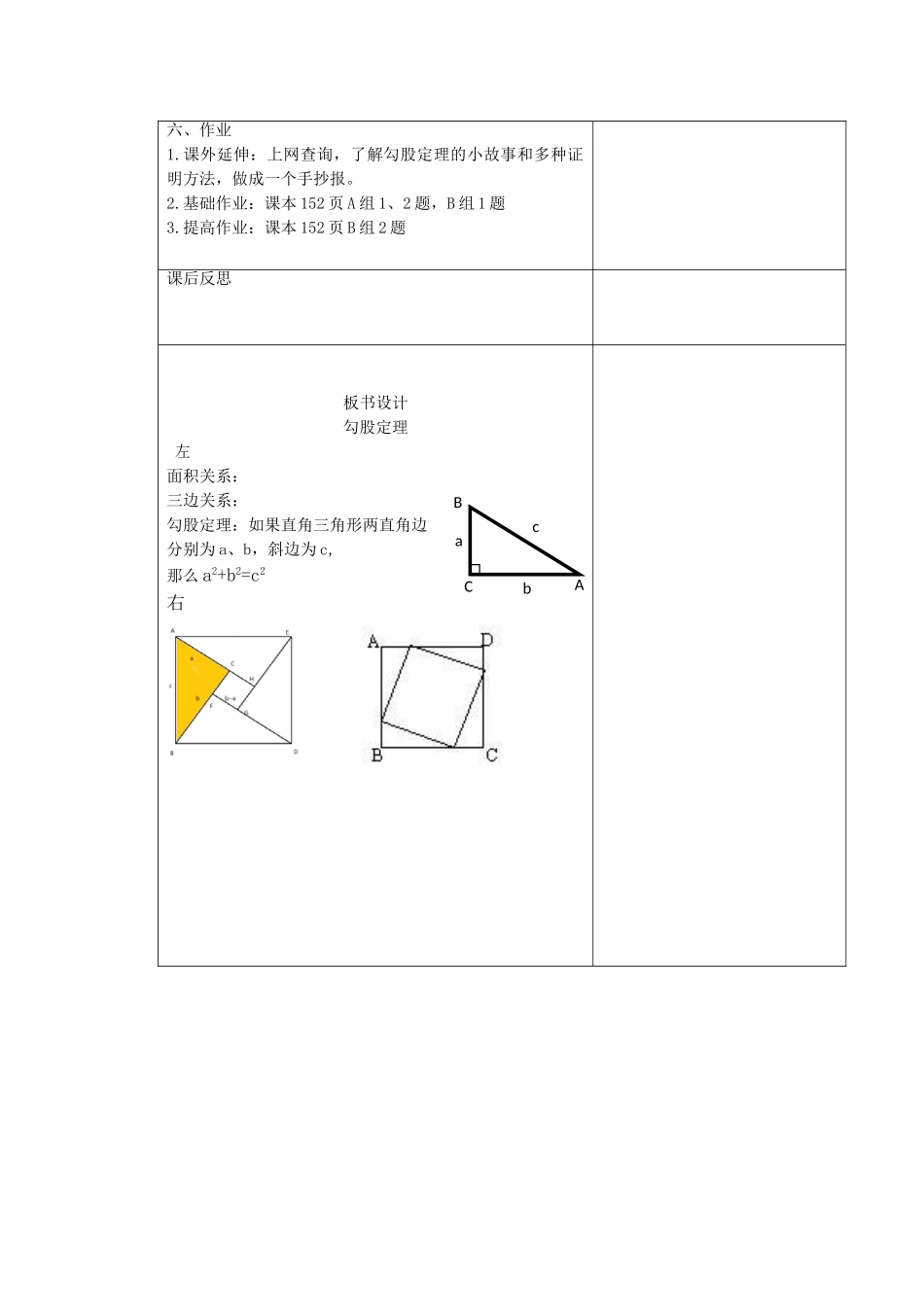
勾股定理【学习目标】1.借助勾股定理的探究过程,体会数形结合思想。发展学生由特殊到一般的合情推理能力。2.借助拼图验证猜想过程,培养直观想象和逻辑推理的数学核心素养。3.掌握勾股定理,能够运用勾股定理解决一些数学问题。【评价任务】1.完成任务1、活动2,指向目标1.2.完成活动3,指向目标2.3.完成活动4,指向目标3.资源与建议本节内容重在引导学生发现和验证勾股定理。勾股定理在数学发展史上具有重要意义。它反映了直角三角形的三边数量关系,是数形结合思想的充分展示。它开启了无理数研究的大门,是解直角三角形的重要工具,在实际生活中有着重要的作用。重点:探索勾股定理的过程。难点:验证勾股定理。学生课前准备:每人准备四个全等的直角三角形,要求:不是等腰直角三角形。学习过程评价标准活动一、数学小故事相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。任务1.学生描述发现的正方形面积之间的关系,进而总结出直角三角形的三边数量关系。活动二、画一画在边长为1的网格纸上做一个直角三角形ABC(非等腰),并以这个直角三角形的三边为边向外做三个正方形(面积分别记为S1、S2、S3)根据图形,回答下列问题:1、分别计算出S1、S2、S3的值;2、S1、S2、S3的数量关系是怎样的?3、直角三角形的三边关系是怎样的?活动三、拼一拼请你以四个全等的直角三角形为工具进行拼图,1、围成一个正方形;2、利用面积关系,验证我们的猜想:1.从小故事入手,引起学生的兴趣。2.能够清楚表达正方形面积之间数量关系,猜想出直角三角形三边关系。3.能够画出图形,发现面积之间数量关系,以及直角三角形三边关系。4.感受一般形状的三角形也有相同的规律。5.能够拼出至少一种图形,能利用等积法给出证明。CBABCAABCa2+b2=c2要求如下:自己先独立思考1分钟,尝试拼图,验证猜想。然后小组交流想法。得出结论:勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2或AC2+BC2=AB2文字表述:直角三角形两直角边的平方和等于斜边的平方。符号表述:Rt△ABC中,∠C=90°则活动四、做一做1.求下列直角三角形中未知边的长:2.如下图,其中所有的四边形都是正方形,所有的三角形都是直角三角形图中数据分别表示其所在正方形的面积,请根据这些数据,分别求出未知的正方形面积A,B和C.五、归纳总结通过这节课,你有哪些收获?在知识上……在学习方法上……6.能够写出...