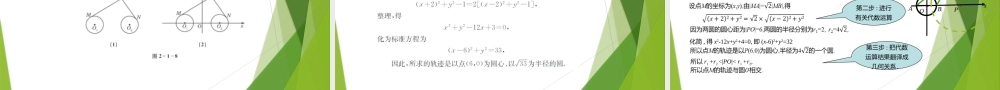2.1圆与圆的位置关系(第4课时)第2章圆锥曲线沪教版2020选修第一册学习目标1.理解圆与圆的位置关系的种类.2.掌握圆与圆的位置关系的代数判断方法与几何判断方法.3.能够利用上述方法判断两圆的位置关系.4.体会根据圆的对称性灵活处理问题的方法和它的优越性.生活中,常见圆与圆的位置关系,如奥运五环、机械零件、生活图案等.从初中的平面几何学习中,我们知道两个圆之间有内含(包括同心)、内切、相交、外切和外离五种位置关系.前面我们运用直线的方程,圆的方程研究了直线与圆的位置关系,现在我们类比上述研究方法,运用圆的方程,通过定量计算研究圆与圆的位置关系。问题思考外离探索新知两个大小不等的圆的位置关系|O1O2|>R+r|O1O2|=R+r|R-r|<|O1O2|
0),圆C2:x2+y2-4ax-2y+4a2=0(a>0).试求a为何值时,两圆C1,C2的位置关系为:(1)相切;(2)相交;(3)外离;(4)内含?思路分析:求出圆心距,与两半径的和或差比较求出a的值.典例1解:圆C1,C2的方程,经配方后可得C1:(x-a)2+(y-1)2=16,C2:(x-2a)2+(y-1)2=1,∴圆心C1(a,1),C2(2a,1),半径r1=4,r2=1.∴|C1C2|=ට(𝑎-2𝑎)2+(1-1)2=a.(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切;当|C1C2|=r1-r2=3,即a=3时,两圆内切.(2)当3<|C1C2|<5,即35,即a>5时,两圆外离.(4)当|C1C2|<3,即0