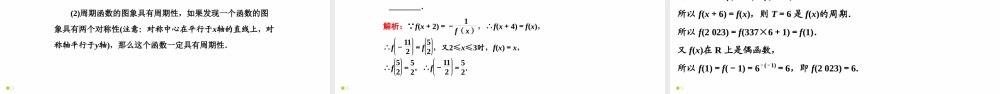数学第1讲函数的奇偶性及周期性高三一轮复习重难点题型题型一函数的奇偶性角度一判断函数的奇偶性判断下列函数的奇偶性.(1)f(x)=x3+x,x∈[-1,4];(2)f(x)=ln2-x2+x;(3)f(x)=x2-1+1-x2;(4)f(x)=x2+2,x>0,0,x=0,-x2-2,x<0.题型一函数的奇偶性【解】(1)因为f(x)=x3+x,x∈[-1,4]的定义域不关于原点对称,所以f(x)既不是奇函数也不是偶函数.(2)f(x)的定义域为(-2,2),f(-x)=ln2+x2-x=-ln2-x2+x=-f(x),所以函数f(x)为奇函数.(3)f(x)的定义域为{-1,1},关于原点对称.又f(-1)=f(1)=0,f(-1)=-f(1)=0,所以f(x)既是奇函数又是偶函数.题型一函数的奇偶性(4)f(x)的定义域为R,关于原点对称,当x>0时,f(-x)=-(-x)2-2=-(x2+2)=-f(x);当x<0时,f(-x)=(-x)2+2=-(-x2-2)=-f(x);当x=0时,f(0)=0,也满足f(-x)=-f(x).故该函数为奇函数.题型一函数的奇偶性[解题技法]判断函数奇偶性的3种常用方法(1)定义法:确定函数的奇偶性时,必须先判定函数定义域是否关于原点对称.若对称,再化简解析式后验证f(-x)=±f(x)或其等价形式f(-x)±f(x)=0是否成立.(2)图象法:题型一函数的奇偶性(3)性质法:设f(x),g(x)的定义域分别是D1,D2,那么在它们的公共定义域上:奇+奇=奇,奇×奇=偶,偶+偶=偶,偶×偶=偶,奇×偶=奇.题型一函数的奇偶性角度二函数奇偶性的应用(1)(2019·高考全国卷Ⅱ)设f(x)为奇函数,且当x≥0时,f(x)=ex-1,则当x<0时,f(x)=()A.e-x-1B.e-x+1C.-e-x-1D.-e-x+1题型一函数的奇偶性(2)(2021·黑龙江哈尔滨师范大学附中月考)已知函数f(x)=cosπ2+2x+xx2+1-1,若f(a)=-13,则f(-a)=()A.13B.23C.-13D.-53题型一函数的奇偶性【解析】(1)通解:依题意得,当x<0时,f(x)=-f(-x)=-(e-x-1)=-e-x+1,选D.优解:依题意得,f(-1)=-f(1)=-(e1-1)=1-e,结合选项知,选D.(2)设g(x)=f(x)+1=-sin2x+xx2+1,易知g(x)是奇函数,则g(a)=f(a)+1=-13+1=23,所以g(-a)=-g(a)=-23,即f(-a)+1=-23,所以f(-a)=-53.故选D.题型一函数的奇偶性[解题技法]与函数奇偶性有关的问题及解题策略(1)求函数的值:利用奇偶性将待求值转化为已知区间上的函数值求解.(2)求函数解析式:先将待求区间上的自变量转化到已知区间上,再利用奇偶性求出,或充分利用奇偶性构造关于f(x)的...