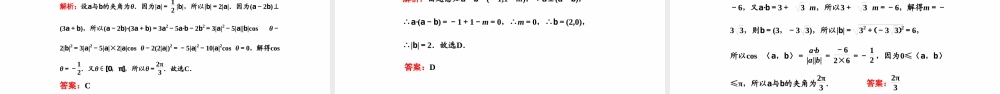数学第3讲平面向量的数量积及应用举例高三一轮复习重难点题型考点一平面向量的数量积的运算[例1](1)(2019·全国卷Ⅱ)已知AB―→=(2,3),AC―→=(3,t),|BC―→|=1,则AB―→·BC―→=()A.-3B.-2C.2D.3(2)(2019·天津高考)在四边形ABCD中,AD∥BC,AB=23,AD=5,∠A=30°,点E在线段CB的延长线上,且AE=BE,则BD―→·AE―→=________.[解析](1) BC―→=AC―→-AB―→=(3,t)-(2,3)=(1,t-3),|BC―→|=1,∴12+t-32=1,∴t=3,∴BC―→=(1,0),∴AB―→·BC―→=2×1+3×0=2.故选C.(2)法一:△AEB为等腰三角形,易得|BE|=2,所以AE―→=AB―→+BE―→=AB―→-25AD―→,则BD―→·AE―→=(AD―→-AB―→)·AB―→-25AD―→=-25AD―→2-AB―→2+75AD―→·AB―→=-10-12+21=-1.法二:如图,以点B为坐标原点,BC所在直线为x轴,垂直BC且过点B的直线为y轴,建立平面直角坐标系,则B(0,0),易知E(-2,0),A(-3,3),又BD=25+12-2×5×23×cos30°=7,所以D(2,3),于是BD―→=(2,3),AE―→=(1,-3),所以BD―→·AE―→=(2,3)·(1,-3)=2-3=-1.[答案](1)C(2)-1[解题技法]求非零向量a,b的数量积的3种方法方法适用范围定义法已知或可求两个向量的模和夹角基底法直接利用定义法求数量积不可行时,可选取合适的一组基底,利用平面向量基本定理将待求数量积的两个向量分别表示出来,进而根据数量积的运算律和定义求解坐标法①已知或可求两个向量的坐标;②已知条件中有(或隐含)正交基底,优先考虑建立平面直角坐标系,使用坐标法求数量积[跟踪训练]1.设向量a=(-1,2),b=(m,1),如果向量a+2b与2a-b平行,那么a与b的数量积等于()A.-72B.-12C.32D.52解析:因为a+2b=(-1+2m,4),2a-b=(-2-m,3),由题意得3(-1+2m)-4(-2-m)=0,解得m=-12,所以a·b=-1×-12+2×1=52.答案:D2.已知向量a,b满足a·(b+a)=2,且a=(1,2),则向量b在a方向上的投影为()A.55B.-55C.-255D.-355解析:由a=(1,2),可得|a|=5,由a·(b+a)=2,可得a·b+a2=2,∴a·b=-3,∴向量b在a方向上的投影为a·b|a|=-355.答案:D3.(2020·湖北汉阳模拟)在△ABC中,|BC|=4,(AB―→+AC―→)·BC―→=0,则BA―→·BC―→=()A.4B.-4C.-8D.8解析:设M为BC的中点,则AB―→+AC―→=2AM―→, (AB―→+AC―→)·BC―→=0...