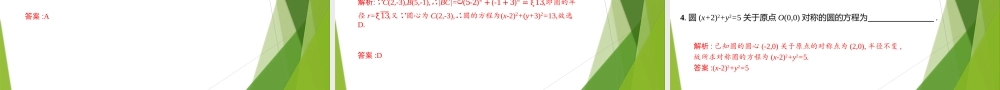2.1圆的标准方程(第1课时)第2章圆锥曲线沪教版2020选修第一册在上一章中,我们初步领略了解析几何的一些基本特点,知道通过建立平面直角坐标系得到直线的方程,然后利用方程讨论点与直线、直线与直线的位置关系.在这一章中,通过对圆锥曲线的研究,我们进一步深入解析几何的核心领域并体验解析几何的威力.对圆锥曲线的研究虽然可以追溯到两千多年前的古希腊时代,但直到笛卡尔坐标系的引入,才找到更一般的且统一的处理方法.在直角坐标平面上,所有圆锥曲线都可以用二元二次方程来表示,从而可以用方程的思想去解决与这些曲线有关的问题.由于圆锥曲线是日常生活中常见的曲线,在航天、航海、光学等领域都有广泛的应用,这使得解析几何成为数学的一个重要分支.除了直线和圆以外,椭圆、双曲线和抛物线已经与平面几何所涉及的内容有本质的区别,但与函数却有了联系,如反比例函数的图像是双曲线、二次函数的图像是抛物线等.在平面几何中已经知道,圆是到一个定点的距离等于定长(大于零)的点的轨迹.这个定点就是圆心,定长就是圆的半径.如果一个圆在直角坐标平面内,我们该如何确定这个圆的位置,并且建立圆的方程呢?1.会用定义推导圆的标准方程,并掌握圆的标准方程的特征.2.能根据所给条件求圆的标准方程.3.掌握点与圆的位置关系并能解决相关问题.学习目标01圆的标准方程02点与圆的位置关系目录月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写.如果把天空看作一个平面,月亮当做一个圆,建立一个平面直角坐标系,那么圆的坐标满足的方程如何表示?《古朗月行》唐李白小时不识月,呼作白玉盘。又疑瑶台镜,飞在青云端。ArxyO情景导入思考1圆是怎样定义的?确定它的要素又是什么呢?各要素与圆有怎样的关系?探究新知定义:平面内到定点的距离等于定长的点的集合叫作圆,定点称为圆心,定长称为圆的半径.确定圆的因素:圆心和半径圆心确定圆的位置,半径确定圆的大小.|MA|=r,由两点间的距离公式,得x-a2+y-b2=r,化简可得:(x-a)2+(y-b)2=r2.AMrxOy思考2已知圆心为A(a,b),半径为你能推导出圆的方程吗?思考3圆心是A(a,b),半径是r的圆的方程是什么?xyOA(a,b)M(x,y)P={M||MA|=r}圆上所有点的集合rbyax22)()(设点M(x,y)为圆A上任一点,则|MA|=r.r思考4是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上?222)()(rbyax点M(x,y)在圆上,由前面讨论可知...