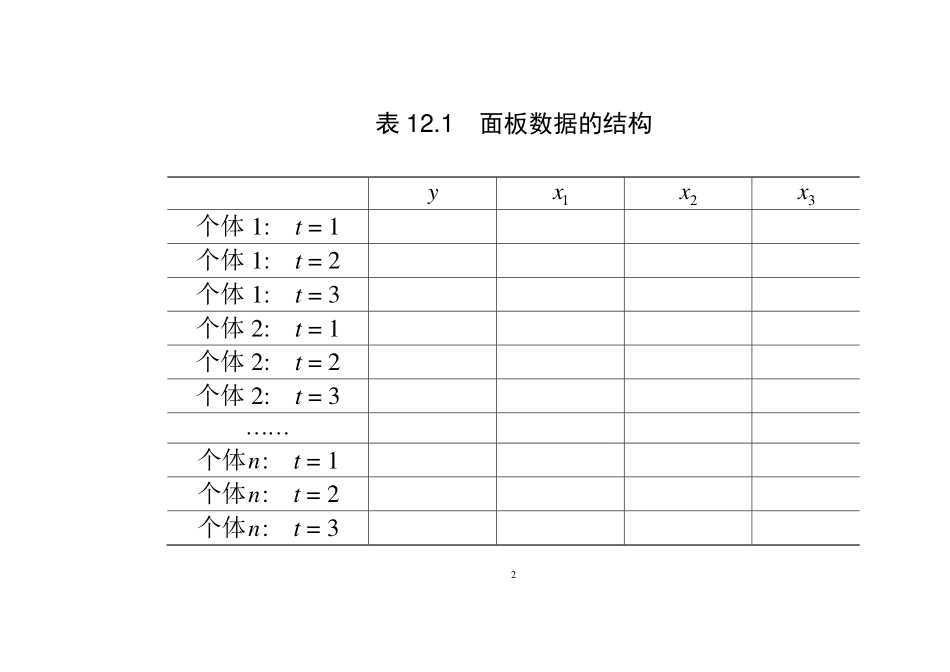
1©陈强,2015年,《计量经济学及Stata应用》,高等教育出版社。第12章面板数据12.1面板数据的特点面板数据(paneldata或longitudinaldata),指在一段时间内跟踪同一组个体(individual)的数据。它既有横截面维度(n位个体),又有时间维度(T个时期)。一个3T的面板数据结构如表12.1。2表12.1面板数据的结构y1x2x3x个体1:t=1个体1:t=2个体1:t=3个体2:t=1个体2:t=2个体2:t=3个体n:t=1个体n:t=2个体n:t=33通常的面板数据T较小,n较大,在使用大样本理论时让n趋于无穷大,称为“短面板”(shortpanel)。如果T较大,n较小,则称为“长面板”(longpanel)。在面板模型中,如果解释变量包含被解释变量的滞后值,称为“动态面板”(dynamicpanel);反之,称为“静态面板”(staticpanel)。本书仅关注静态面板。在面板数据中,如果每个时期在样本中的个体完全一样,则称为“平衡面板”(balancedpanel);反之,则称为“非平衡面板”(unbalancedpanel)。主要关注平衡面板,但在本章第11节讨论非平衡面板。4面板数据的主要优点如下。(1)有助于解决遗漏变量问题:遗漏变量常由不可观测的个体差异或“异质性”(heterogeneity)造成(比如个体能力)。如果个体差异“不随时间而改变”(timeinvariant),则面板数据提供了解决遗漏变量问题的又一利器。(2)提供更多个体动态行为的信息:面板数据有横截面与时间两个维度,可解决截面数据或时间序列不能解决的问题。5例如何区分规模效应与技术进步对企业生产效率的影响。截面数据没有时间维度,无法观测到技术进步。单个企业的时间序列数据,也无法区分生产效率提高有多少由于规模扩大,有多少由于技术进步。例对于失业问题,截面数据告诉我们在某个时点上哪些人失业,时间序列告诉我们某个人就业与失业的历史,但均无法告诉我们是否失业的总是同一批人(低流转率),还是失业的人群总在变动(高流转率)。如有面板数据,就可能解决上述问题。(3)样本容量较大:同时有截面与时间维度,面板数据的样本容量通常更大,可提高估计精度。6面板数据也会带来问题。样本数据通常不满足iid假定,因为同一个体在不同期的扰动项一般存在自相关。面板数据的收集成本通常较高,不易获得。12.2面板数据的估计策略一个极端策略是,将面板看成截面数据进行混合回归(pooledregression),即要求样本中每位个体拥有完全相同的回归方程。混合回归的缺点是,忽略个体不可观测的异质性(heterogeneity),而该异质性可能与解释变量相关,导致估计不一致。7...