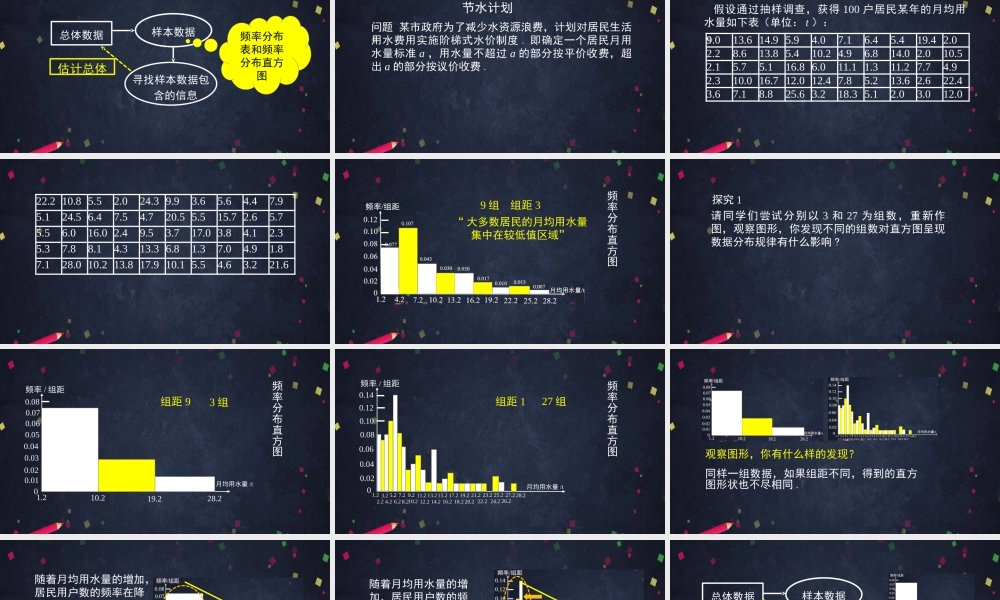
高一年级数学总体取值规律的估计(二)主讲人赵月灵北京市通州区潞河中学总体数据寻找样本数据包含的信息样本数据估计总体频率分布表和频率分布直方图问题某市政府为了减少水资源浪费,计划对居民生活用水费用实施阶梯式水价制度.即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.节水计划假设通过抽样调查,获得100户居民某年的月均用水量如下表(单位:t):9.013.614.95.94.07.16.45.419.42.02.28.613.85.410.24.96.814.02.010.52.15.75.116.86.011.11.311.27.74.92.310.016.712.012.47.85.213.62.622.43.67.18.825.63.218.35.12.03.012.022.210.85.52.024.39.93.65.64.47.95.124.56.47.54.720.55.515.72.65.75.56.016.02.49.53.717.03.84.12.35.37.88.14.313.36.81.37.04.91.87.128.010.213.817.910.15.54.63.221.6频率分布直方图9组组距3“大多数居民的月均用水量集中在较低值区域”请同学们尝试分别以3和27为组数,重新作图,观察图形,你发现不同的组数对直方图呈现数据分布规律有什么影响?探究1月均用水量/t0.010.020.030.040.051.210.219.228.20频率/组距0.060.070.08组距93组频率分布直方图月均用水量/t0.020.140.040.080频率/组距0.060.100.121.22.23.25.214.26.27.24.29.212.211.218.215.213.217.219.221.223.225.227.228.222.220.224.226.216.210.28.2组距127组频率分布直方图观察图形,你有什么样的发现?同样一组数据,如果组距不同,得到的直方图形状也不尽相同.随着月均用水量的增加,居民用户数的频率在降低.月均用水量在区间[1.2,10.2)内的用户频率远大于其他两个区间内的频率.组距93组这说明大部分居民的月均用水量都小于10.2吨.随着月均用水量的增加,居民用户数的频率呈现下降趋势.主要集中在低值区,尤其区间[5.2,6.2)最集中.但存在个别区间频率变大或缺失的现象.组距127组总体数据寻找样本数据包含的信息样本数据估计总体不同的分组对样本估计总体有什么影响?结论:随着月均用水量的增加,居民用户数的频率呈现下降趋势.共同点整体规律结论:容易看出数据的分布整体特点.无法看到每组数据的分布,损失了很多原始数据.优点缺点不同点结论:保留较多原始信息.不容易看出总体的分布特点.优点缺点不同点结论:组数太多或太少都会影响对总体的判断,因此我们要根据实际情况合理分组,不断积累数据分组、合理使用图表的经验.折线图扇形图直方图条形图条形图、扇形图、折线图、直方图,这些统计...