课时3370_3.2.1双曲线及其标准方程（第一课时）-(许苏华)3.2.1 双曲线及其标准方程（第一课时）【公众号悦过学习分享】(1).pptxVIP免费

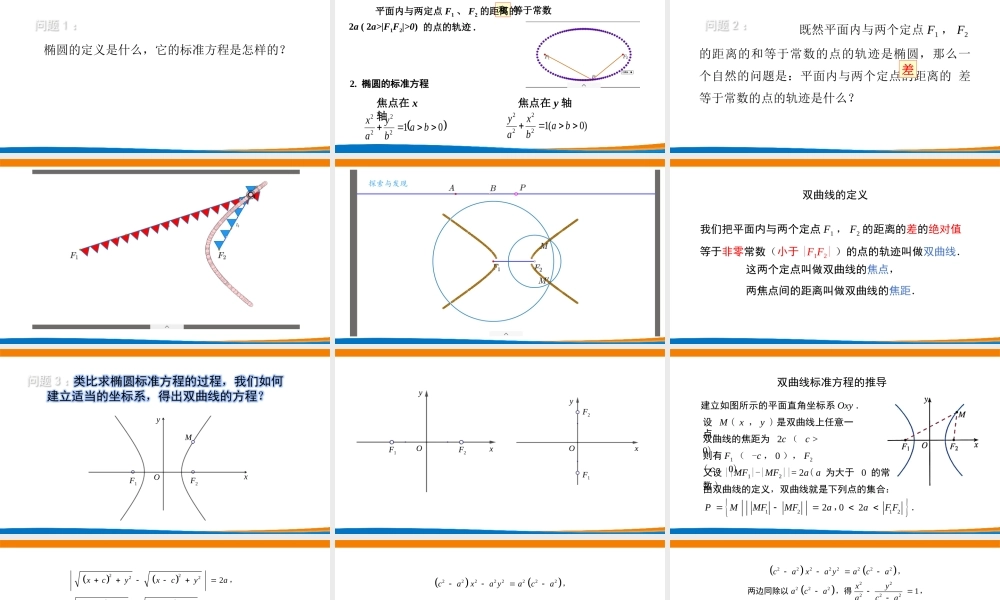
（第一课时）主讲人：深圳中学许苏华深圳市新课程新教材高中数学在线教学3.2.1双曲线及其标准方程椭圆的定义是什么，它的标准方程是怎样的？问题1：1.椭圆的定义和等于常数2a(2a>|F1F2|>0)的点的轨迹.平面内与两定点F1、F2的距离的2.椭圆的标准方程)0(12222babxay012222babyax焦点在y轴焦点在x轴既然平面内与两个定点F1，F2的距离的和等于常数的点的轨迹是椭圆，那么一个自然的问题是：平面内与两个定点的距离的差等于常数的点的轨迹是什么？差问题2：双曲线的定义我们把平面内与两个定点F1，F2的距离的差的绝对值等于非零常数（小于|F1F2|）的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．F1F2MxyO类比求椭圆标准方程的过程，我们如何建立适当的坐标系，得出双曲线的方程？问题3：F1F2xyOF1F2xyO双曲线标准方程的推导建立如图所示的平面直角坐标系Oxy．设M(x，y)是双曲线上任意一点，双曲线的焦距为2c（c>0)，则有F1（-c，0），F2(c，0).又设||MF1|-|MF2||=2a(a为大于0的常数)．由双曲线的定义，双曲线就是下列点的集合：1212202PMMFMFaaFF，．22222xcyxcya，22222xcyxcya，①222222222222222xcyaxcyxcyaxcycxaaxcy，，，两边平方，整理得：22222222caxayaca，讨论以上方程的变形是不是同解变形？类似于椭圆，能不能给出结构简单且优美的方程呢？问题4：双曲线上任意一点的坐标（x，y）都是方程②的解；以方程②的解为坐标的点（x，y）与双曲线的两个焦点F1（-c，0），F2（c，0）的距离之差的绝对值都为2a，22222222caxayaca，222222221两边同除以得xyacaaca，，22220由双曲线的定义知即所以cacaca，，，．2220类比椭圆标准方程的建立过程令bcab，，2222100xyabab，．②即以方程②的解为坐标的点都在双曲线上．我们称方程②是双曲线的方程，这个方程叫做双曲线的标准方程.它表示焦点在x轴上，两个焦点分别是F1（-c，0），F2（c，0）的双曲线，这里．222cab2222100xyabab，．②类比焦点在轴上的椭圆标准方程焦点在轴的双曲线的标准方程是什么yy，？如图，双曲线的焦距为2c，焦点分别是F1（0，-c），F2（0，c）．a，b的意义同上，这时双曲线的...