课时21861_7.2.3离散型随机变量方差-7.3.2离散型随机变量的方差【公众号悦过学习分享】(1).pptVIP免费

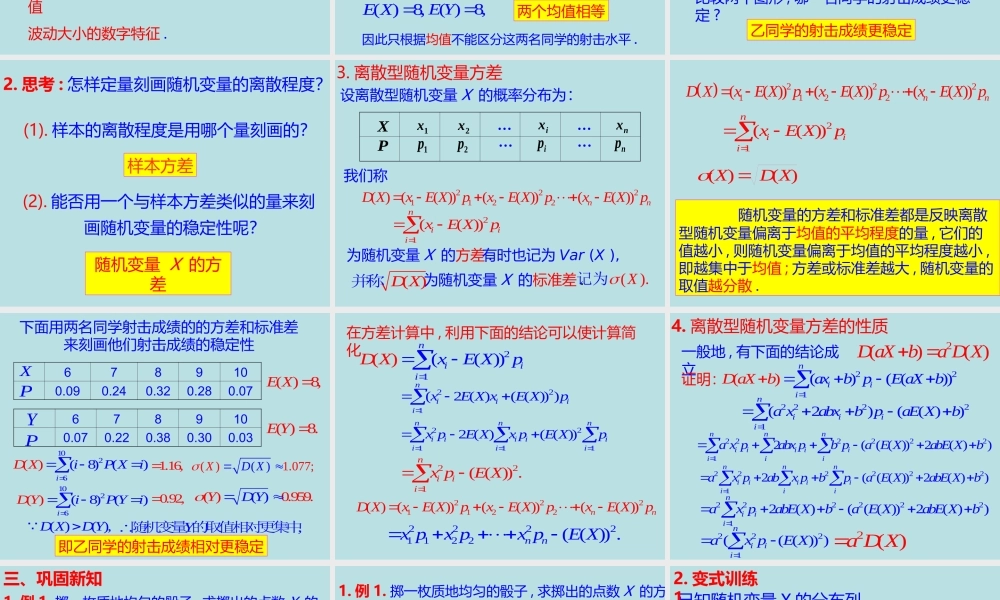
7.3.2离散型随机变量的方差高二数学选择性必修第三册第七章随机变量及其分布主讲老师：宋武学习目标1.理解取有限个值的离散型随机变量方差及标准差的概念与意义;2.掌握方差的性质,能计算简单离散型随机变量的方差,并能解决一些简单的实际问题;3.核心素养:数据分析、逻辑推理、数学运算。1.离散型随机变量的数学期望2.数学期望的性质bXaEbaXE)()(P1xix2x······1p2pip······nxnpX数学期望是反映离散型随机变量的平均水平一、回顾旧知iniinnpxpxpxpxXE12211)(3.样本方差])()()[(1222212xxxxxxnsn叫做这组数据的方差.xnxxx,,,21设在一组数据中,是它们是它们的平均数,那么随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小.所以我们还需要寻找反映随机变量取值波动大小的数字特征.如何评价这两名同学的射击水平？因此只根据均值不能区分这两名同学的射击水平.二、探究新知1.问题2.从两名同学中挑选出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列为6789100.090.240.320.280.076789100.070.220.380.300.03XPYP,8)(XE,8)(YE两个均值相等比较两个图形,哪一名同学的射击成绩更稳定?除平均中靶环数以外,还要考虑稳定性,即击中环数的离散程度.乙同学的射击成绩更稳定下图分别是X和Y的概率分布图.YP0.310987060.40.20.1XP0.310987060.40.20.12.思考:怎样定量刻画随机变量的离散程度？(1).样本的离散程度是用哪个量刻画的？样本方差(2).能否用一个与样本方差类似的量来刻画随机变量的稳定性呢？随机变量X的方差3.离散型随机变量方差设离散型随机变量X的概率分布为：我们称为随机变量X的方差.P1xix2x······1p2pip······nxnpX为随机变量X的标准差.nnpXExpXExpXExXD2222121))(())(())(()(()DX并称().X记为niiipXEx12))((有时也记为Var(X),随机变量的方差和标准差都是反映离散型随机变量偏离于均值的平均程度的量,它们的值越小,则随机变量偏离于均值的平均程度越小,即越集中于均值;方差或标准差越大,随机变量的取值越分散.2221122(())(())(())nnDXxEXpxEXpxEXpniiipXEx12))(()()(XDX6789100.090.240.320.280.076789100.070.220.380.300.03XPYP,8)(XE.8)(YE1026(8)()()...