课时3326_1.1.2空间向量的数量积（第一课时）-1.1.2 空间向量的数量积运算（第1课时）【公众号悦过学习分享】(1).pptxVIP免费

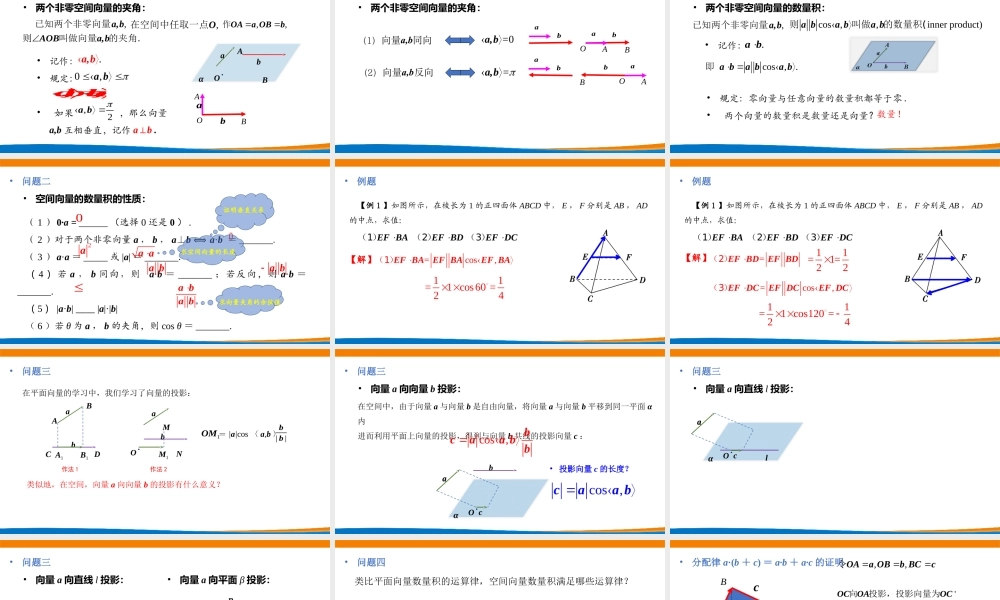
（第一课时）主讲人：深圳市龙华高级中学王子淳深圳市新课程新教材高中数学在线教学1.1.2空间向量的数量积运算•记作：•规定：•如果，那么向量a,b互相垂直，记作a⊥b.•问题一•两个非零空间向量的夹角：ba.OαAB,已知两个非零向量a,b,在空间中任取一点O,,�作OAaOBb则叫做向量的夹角.AOBa,b.a,b0,ababba,,＝,2abaOAbB•问题一•两个非零空间向量的夹角：ababOABabOaAbB=0a,b=a,b•记作：•问题二•两个非零空间向量的数量积：,已知两个非零向量a,bcos,,innerproduct)则叫做的数量积(ababab.abcos,.即ababab•规定：零向量与任意向量的数量积都等于零.•两个向量的数量积是数量还是向量？数量!•问题二（1）0·a=（选择0还是0）.（2）对于两个非零向量a，b，a⊥b⟺a·b＝_______.（3）a·a＝_____或|a|＝_______.（4）若a，b同向，则a·b＝_______；若反向，则a·b＝_______.（5）|a·b|____|a|·|b|（6）若θ为a，b的夹角，则cosθ＝_______.aa•空间向量的数量积的性质：02aabababab0证明垂直关系求空间向量的长度求向量夹角的余弦值•例题【例1】如图所示，在棱长为1的正四面体ABCD中，E，F分别是AB，AD的中点，求值：�（1）EFBA�（2）EFBD�（3）EFDC=cos,�（1）EFBAEFBAEFBA11=1cos60=24【解】•例题【例1】如图所示，在棱长为1的正四面体ABCD中，E，F分别是AB，AD的中点，求值：�（1）EFBA�（2）EFBD�（3）EFDC=�（2）EFBDEFBD11=1=22=cos,�（3）EFDCEFDCEFDC11=1cos120=24【解】在平面向量的学习中，我们学习了向量的投影：baABA1DCB1ba.ONMM1＝|a|cos〈a,b〉||bb1�OM类似地，在空间，向量a向向量b的投影有什么意义？•问题三作法1作法2在空间中，由于向量a与向量b是自由向量，将向量a与向量b平移到同一平面α内进而利用平面上向量的投影，得到与向量b共线的投影向量c：•问题三ba.Oαac•向量a向向量b投影：cos,bcaabb•投影向量c的长度？cos,caab•问题三•向量a向直线l投影：la.Oαac•问题三•向量a向直线l投影：•向量a向平面β投影：caABA1B1a注：向量a与投影向量c的夹角就是向量a所在的直线与平面β所成的角类比平面向量数量积的运算律，空间向量数量积满足哪些运算律？•问题四数乘向量与向量数量积的结合律(λa)·b＝λ(a·b),λR∈交换律a·b＝b·a分配律a·(b＋c)＝a·b＋a·c•平面...