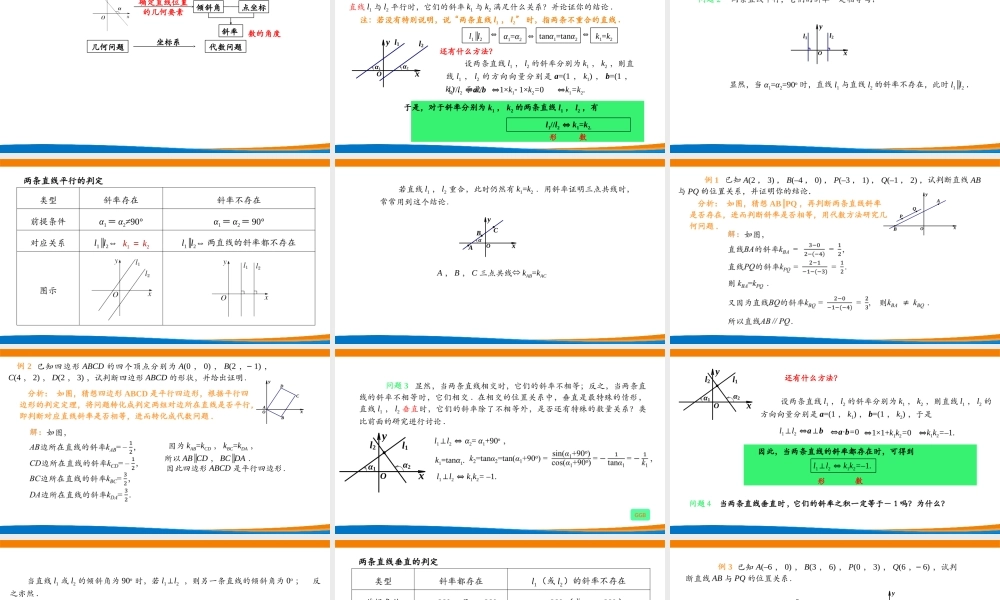
主讲人:深圳科学高中唐雪梅深圳市新课程新教材高中数学在线教学2.1.2两条直线平行和垂直的判定一、复习引入倾斜角确定直线位置的几何要素斜率点坐标几何问题代数问题1.直线的倾斜角:0180;2.直线的斜率:tan(90)k;3.斜率公式:2121yykxx,(其中11122212(,),(,)()PxyPxyxx为直线上两点);4.若直线l的斜率为k,则它的一个方向向量为(1,)k.数的角度坐标系问题1我们知道,平面中的两条直线有两种位置关系:相交、平行.当两条直线l1与l2平行时,它们的斜率k1与k2满足什么关系?并论证你的结论.注:若没有特别说明,说“两条直线l1,l2”时,指两条不重合的直线.l2α2Oyxl1α1设两条直线l1,l2的斜率分别为k1,k2,则直线l1,l2的方向向量分别是a=(1,k1),b=(1,k2),于是l1//l2⇔a//b⇔1×k11×k2=0⇔k1=k2.l1∥l2tanα1=tanα2α1=α2k1=k2数形⇔⇔⇔l1//l2⇔k1=k2.于是,对于斜率分别为k1,k2的两条直线l1,l2,有还有什么方法?二、新知探究显然,当α1=α2=90o时,直线l1与直线l2的斜率不存在,此时l1∥l2.l2l1Oyx问题2两条直线平行,它们的斜率一定相等吗?类型斜率存在斜率不存在前提条件α1=α2≠90°α1=α2=90°对应关系l1∥l2⇔l1∥l2⇔两直线的斜率都不存在图示k1=k2两条直线平行的判定若直线l1,l2重合,此时仍然有k1=k2.用斜率证明三点共线时,常常用到这个结论.BOyxACαA,B,C三点共线⇔kAB=kAC例1已知A(2,3),B(–4,0),P(–3,1),Q(–1,2),试判断直线AB与PQ的位置关系,并证明你的结论.分析:如图,猜想ABPQ∥,再判断两条直线斜率是否存在,进而判断斜率是否相等,用代数方法研究几何问题.QPBAxyODCBAxyO例2已知四边形ABCD的四个顶点分别为A(0,0),B(2,–1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.因为kAB=kCD,kBC=kDA,所以AB∥CD,BC∥DA.因此四边形ABCD是平行四边形.分析:如图,猜想四边形ABCD是平行四边形,根据平行四边形的判定定理,将问题转化成判定两组对边所在直线是否平行,即判断对应直线斜率是否相等,进而转化成代数问题.问题3显然,当两条直线相交时,它们的斜率不相等;反之,当两条直线的斜率不相等时,它们相交.在相交的位置关系中,垂直是最特殊的情形,直线l1,l2垂直时,它们的斜率除了不相等外,是否还有特殊的数量关系?类比前面的研究进行讨论.l2α2l1α1xyOGGBl1⊥l2⇔α2=α1+90o,k1=tanα1.l1⊥l2⇔k1k2=–1.l2α2l1α1xyO还有什...