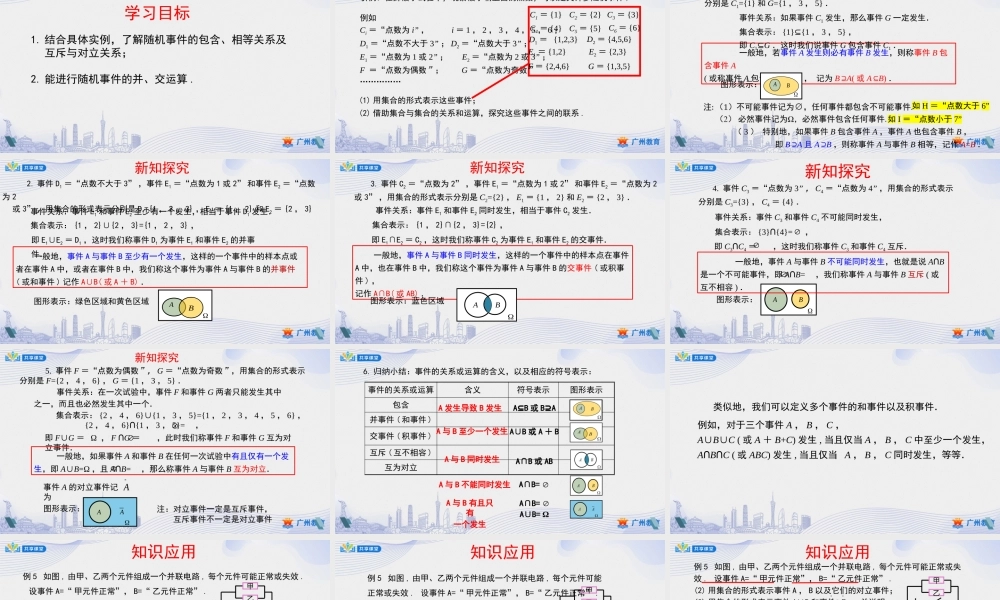
高一—人教A版—数学—必修第二册—第十章广州市花都区秀全中学贾丽10.1.2事件的关系和运算学习目标1.结合具体实例,了解随机事件的包含、相等关系及互斥与对立关系;2.能进行随机事件的并、交运算.例如Ci=“点数为i”,i=1,2,3,4,5,6;D1=“点数不大于3”;D2=“点数大于3”;E1=“点数为1或2”;E2=“点数为2或3”;F=“点数为偶数”;G=“点数为奇数”……………(1)用集合的形式表示这些事件;引例:在掷骰子试验中,观察骰子朝上面的点数,可以定义许多随机事件,C1={1}C2={2}C3={3}C4={4}C6={6}C5={5}D1={1,2,3}D2={4,5,6}E1={1,2}E2={2,3}F={2,4,6}G={1,3,5}(2)借助集合与集合的关系和运算,探究这些事件之间的联系.新课引入一般地,若事件A发生则必有事件B发生,则称事件B包含事件A(或称事件A包含于事件B),记为B⊇A(或A⊆B).1.事件C1="点数为1"和事件G="点数为奇数",用集合的形式表示分别是C1={1}和G={1,3,5}.事件关系:如果事件C1发生,那么事件G一定发生.集合表示:{1}⊆{1,3,5},即C1⊆G.这时我们说事件G包含事件C1.(3)特别地,如果事件B包含事件A,事件A也包含事件B,即B⊇A且A⊇B,则称事件A与事件B相等,记作A=B.AB图形表示:新知探究如H=“点数大于6”如I=“点数小于7”一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或者在事件A中,或者在事件B中,我们称这个事件为事件A与事件B的并事件(或和事件)记作A∪B(或A+B).2.事件D1=“点数不大于3”,事件E1=“点数为1或2”和事件E2=“点数为2或3”,用集合的形式表示分别是D1={1,2,3},E1={1,2}和E2={2,3}事件关系:事件E1和事件E2至少有一个发生,相当于事件D1发生.集合表示:{1,2}∪{2,3}={1,2,3},即E1∪E2=D1,这时我们称事件D1为事件E1和事件E2的并事件.AB图形表示:绿色区域和黄色区域新知探究一般地,事件A与事件B同时发生,这样的一个事件中的样本点在事件A中,也在事件B中,我们称这个事件为事件A与事件B的交事件(或积事件),记作A∩B(或AB).3.事件C2=“点数为2”,事件E1=“点数为1或2”和事件E2=“点数为2或3”,用集合的形式表示分别是C2={2},E1={1,2}和E2={2,3}.事件关系:事件E1和事件E2同时发生,相当于事件C2发生.集合表示:{1,2}∩{2,3}={2},即E1∩E2=C2,这时我们称事件C2为事件E1和事件E2的交事件.AB图形表示:蓝色区域新知探究4.事件C3=“点数为3”,C4=“点数为...