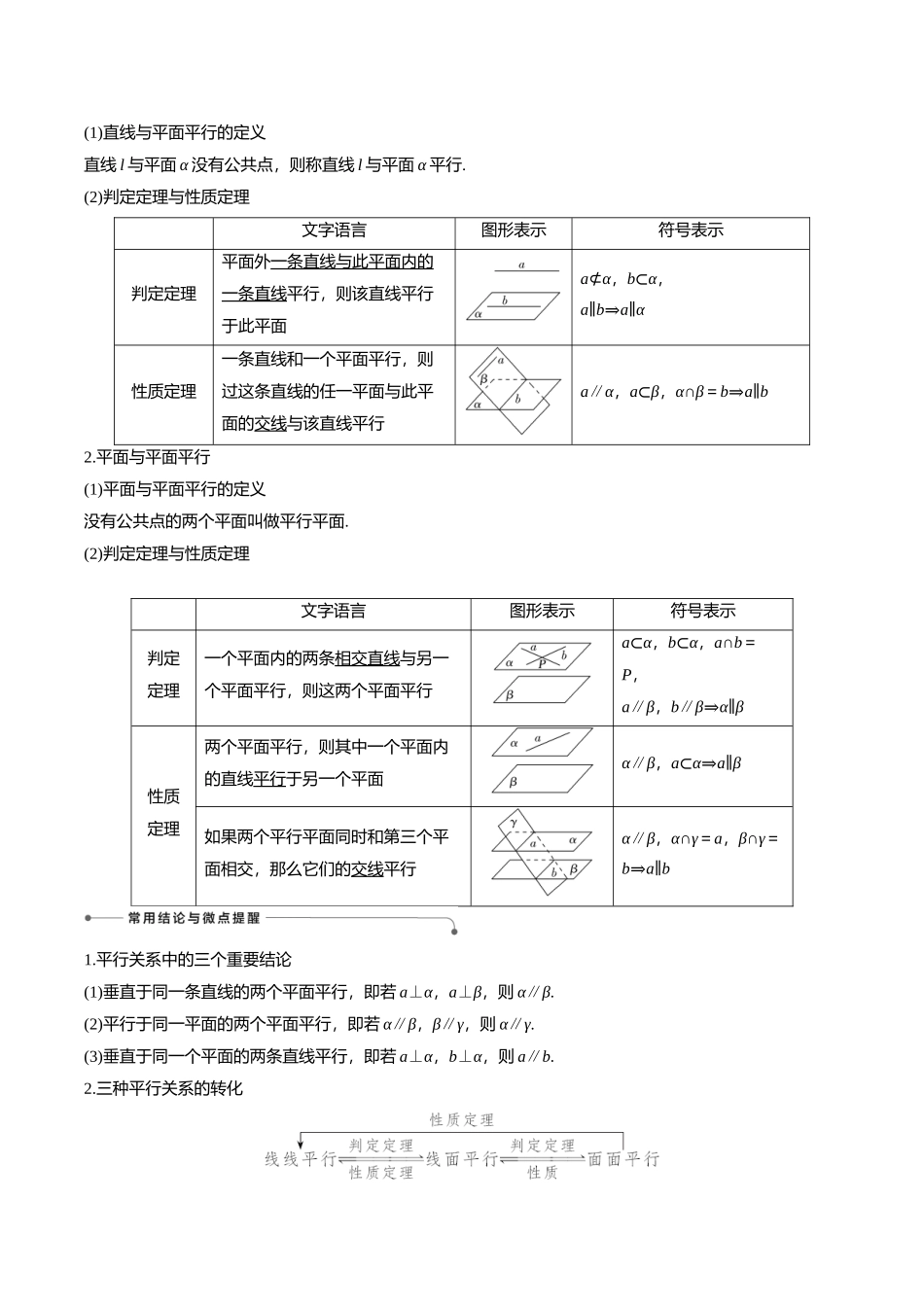
7.2空间中的平行关系教学设计(人教A版普通高中教科书数学必修第二册第八章)深圳第二外国语学校靳建芳一、教学目标:1、知识与技能目标:通过复习三个平行的关系,使学生在《立体几何》的证明中能够正确运用定理证明三个平行,从而使学生重新认识学习立体几何的目的,明确立体几何研究的内容;使学生初步建立空间观念,会看空间图形的直观图;使学生知道立体几何研究问题的一般思想方法。2、过程与方法目标:通过对具体情形的分析,归纳得出一般规律,让学生具备初步归纳能力;借助图形,通过整体观察、直观感知,使学生形成积极主动、勇于探索的学习方式,完善思维结构,发展空间想象能力。3、情感、态度、与价值观目标:在教学过程中培养学生创新意识和数学应用意识,提高学生学习数学的兴趣并注意在小组合作学习中培养学生的合作精神。二、教学重点与难点:重点:培养空间想象能力,明确证明空间中的平行关系的一般思想方法,并会应用。难点:在证明的过程中做辅助线或辅助平面。三、教学方法:引导式教学法四、学情分析:1、由于这是复习课,学生已经系统学习了立体几何的知识,本节课就是让学生更深入地对空间中几何图形的平行位置和数量关系进行推理和计算;2、学生在学习过程中将会遇到一些问题:不能很好地使用直观图来表示立体图形、不能准确的做出辅助线、证明过程书写不规范等等。五、教学过程:(一)考纲要求:(1)以空间直线、平面位置关系的定义为出发点认识和理解空间中的平行关系;(2)理解直线和平面平行、平面和平面平行的判定定理与性质定理;(3)能用公理、定理和已经获得的结论证明一些空间位置关系的简单命题。设计意图:明确考纲要求,做到心中有数;(二)知识梳理:1.直线与平面平行(1)直线与平面平行的定义直线l与平面α没有公共点,则称直线l与平面α平行.(2)判定定理与性质定理文字语言图形表示符号表示判定定理平面外一条直线与此平面内的一条直线平行,则该直线平行于此平面a⊄α,b⊂α,a∥b⇒a∥α性质定理一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行a∥α,a⊂β,α∩β=b⇒a∥b2.平面与平面平行(1)平面与平面平行的定义没有公共点的两个平面叫做平行平面.(2)判定定理与性质定理文字语言图形表示符号表示判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行a⊂α,b⊂α,a∩b=P,a∥β,b∥β⇒α∥β性质定理两个平面平行,则其中一个平面内的直线平行...