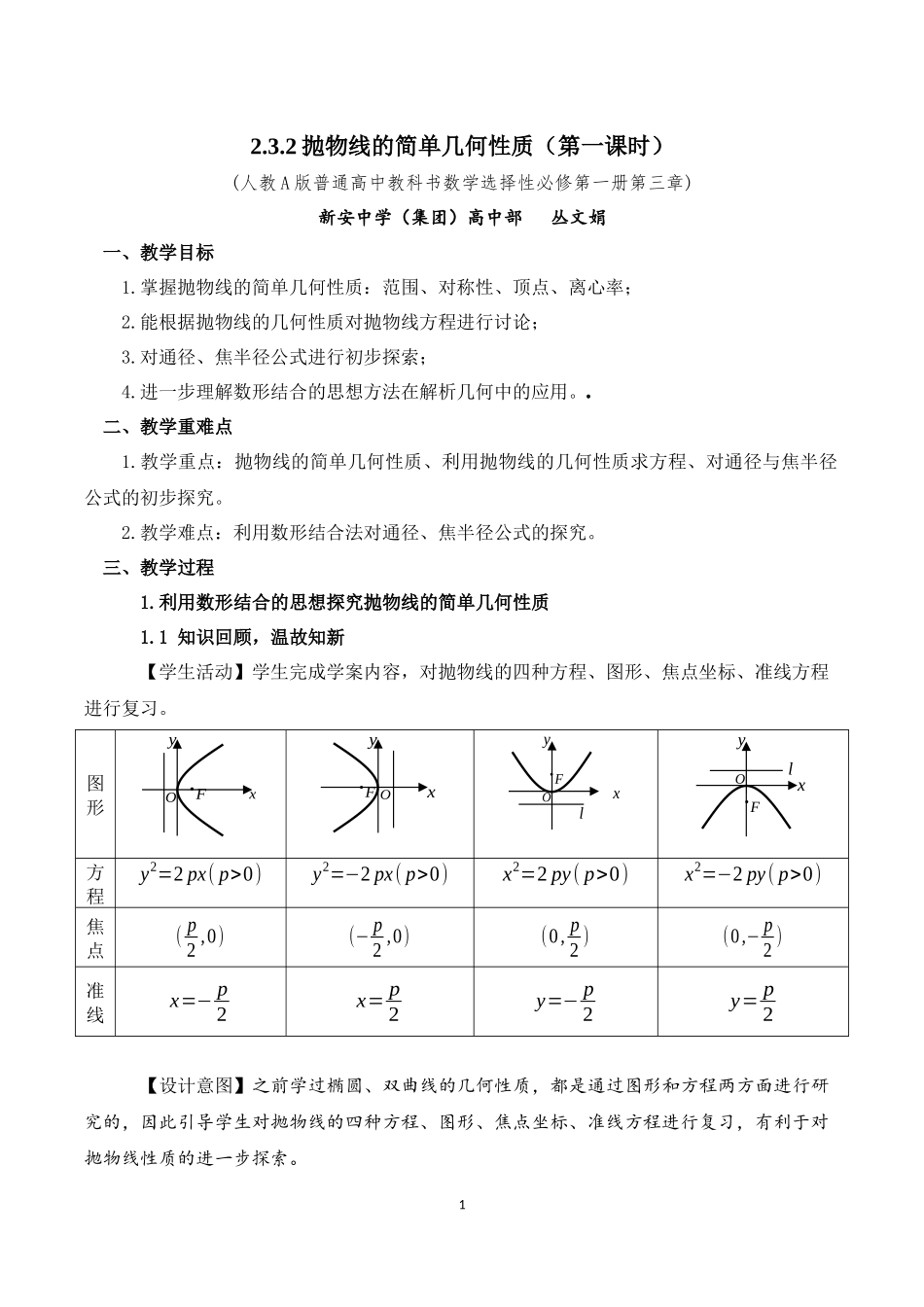
12.3.2抛物线的简单几何性质(第一课时)(人教A版普通高中教科书数学选择性必修第一册第三章)新安中学(集团)高中部丛文娟一、教学目标1.掌握抛物线的简单几何性质:范围、对称性、顶点、离心率;2.能根据抛物线的几何性质对抛物线方程进行讨论;3.对通径、焦半径公式进行初步探索;4.进一步理解数形结合的思想方法在解析几何中的应用。奎屯王新敞新疆二、教学重难点1.教学重点:抛物线的简单几何性质、利用抛物线的几何性质求方程、对通径与焦半径公式的初步探究。2.教学难点:利用数形结合法对通径、焦半径公式的探究。三、教学过程1.利用数形结合的思想探究抛物线的简单几何性质1.1知识回顾,温故知新【学生活动】学生完成学案内容,对抛物线的四种方程、图形、焦点坐标、准线方程进行复习。图形方程y2=2px(p>0)y2=−2px(p>0)x2=2py(p>0)x2=−2py(p>0)焦点(p2,0)(−p2,0)(0,p2)(0,−p2)准线x=−p2x=p2y=−p2y=p2【设计意图】之前学过椭圆、双曲线的几何性质,都是通过图形和方程两方面进行研究的,因此引导学生对抛物线的四种方程、图形、焦点坐标、准线方程进行复习,有利于对抛物线性质的进一步探索。xOyFxyOFxFylOxylOF21.2数形结合,类比探究问题1:类比用标准方程研究椭圆、双曲线几何性质的过程与方法,请思考:我们要研究抛物线的哪些几何性质?如何研究这些性质?【预设答案】前面我们学习了椭圆、双曲线的范围、对称性、顶点、离心率,在双曲线中还学习了渐近线。我们是通过“数”和“形”两方面对椭圆、双曲线的几何性质进行探究的。【设计意图】类比椭圆、双曲线几何性质的研究思路,为接下来用数形结合法研究抛物线的几何性质进行铺垫。问题2:观察图形,你能发现抛物线横、纵坐标的取值范围吗?【预设答案】通过观察图形,学生很容易得到开口向右的抛物线中横、纵坐标的取值范围,即为问题3:从数的角度,也就是从抛物线方程的角度,怎样得到抛物线中横纵坐标的取值范围呢?【预设答案】在方程中,并无限制,因此。而因为,且,所以。【设计意图】让学生从“数”和“形”两个角度探索抛物线的范围。问题4:观察图形,抛物线有几条对称轴?是否有对称中心?3【预设答案】学生观察图形容易得到开口向右的抛物线关于轴对称,没有对称中心。问题5:从“数”的角度,怎样说明抛物线图像关于x轴对称?【教师讲授】要说明抛物线的图像关于x轴对称,只需要在抛物线上任取一点,关于x轴的对称点也在抛物线上即可。【设计意图】引导...