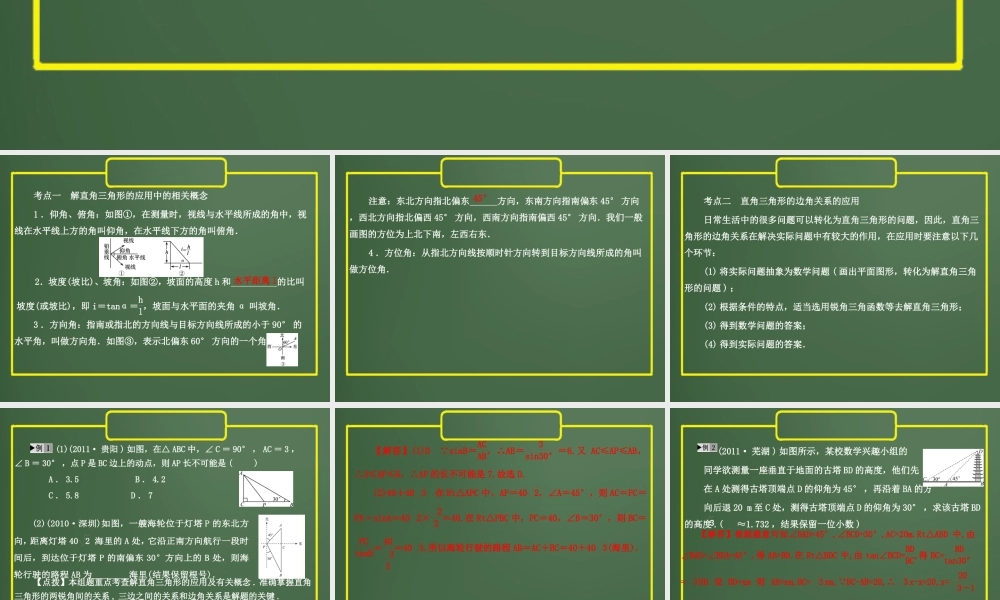
三角函数的应用考点知识精讲中考典例精析考点训练举一反三考点一解直角三角形的应用中的相关概念1.仰角、俯角:如图①,在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角.3.方向角:指南或指北的方向线与目标方向线所成的小于90°的水平角,叫做方向角.如图③,表示北偏东60°方向的一个角.2.坡度(坡比)、坡角:如图②,坡面的高度h和的比叫坡度(或坡比),即i=tanα=hl,坡面与水平面的夹角α叫坡角.水平距离l注意:东北方向指北偏东方向,东南方向指南偏东45°方向,西北方向指北偏西45°方向,西南方向指南偏西45°方向.我们一般画图的方位为上北下南,左西右东.4.方位角:从指北方向线按顺时针方向转到目标方向线所成的角叫做方位角.45°考点二直角三角形的边角关系的应用日常生活中的很多问题可以转化为直角三角形的问题,因此,直角三角形的边角关系在解决实际问题中有较大的作用,在应用时要注意以下几个环节:(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;(3)得到数学问题的答案;(4)得到实际问题的答案.(1)(2011·贵阳)如图,在△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是()A.3.5B.4.2C.5.8D.7【点拨】本组题重点考查解直角三角形的应用及有关概念.准确掌握直角三角形的两锐角间的关系,三边之间的关系和边角关系是解题的关键.(2)(2010·深圳)如图,一艘海轮位于灯塔P的东北方向,距离灯塔402海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为________海里(结果保留根号).【解答】(1)D sinB=ACAB,∴AB=3sin30°=6.又AC≤AP≤AB,∴3≤AP≤6,∴AP的长不可能是7.故选D.(2)40+403在Rt△APC中,AP=402,∠A=45°,则AC=PC=PA·sinA=402×22=40.在Rt△PBC中,PC=40,∠B=30°,则BC=PCtanB=4033=403.所以海轮行驶的路程AB=AC+BC=40+403(海里).(2011·芜湖)如图所示,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退20m至C处,测得古塔顶端点D的仰角为30°,求该古塔BD的高度.(≈1.732,结果保留一位小数)3【解答】根据题意可知∠BAD=45°,∠BCD=30°,AC=20m.Rt△ABD中,由∠BAD=∠BDA=45°,得AB=BD.在Rt△BDC...