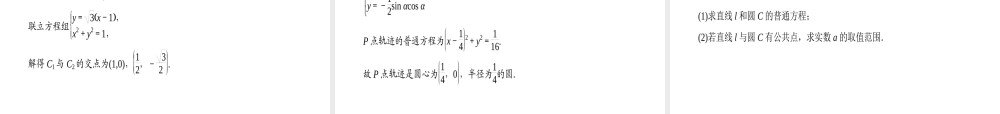参数方程第二讲•2.1曲线的参数方程2.1.2参数方程的概念与圆的参数方程栏目导航课前教材预案课堂深度拓展课后限时作业课末随堂演练•曲线的参数方程和普通方程是曲线方程的不同形式.一般地,可以通过__________而从参数方程得到普通方程.课前教材预案•要点一参数方程转化为普通方程消去参数•要点二普通方程转化为参数方程如果知道变数x,y中的一个与参数t的关系,例如__________,把它代入普通方程,求出另一个变数与参数的关系_________,那么x=ft,y=gt就是曲线的参数方程.在参数方程与普通方程的互化中,必须使x,y的____________保持一致.x=f(t)y=g(t)取值范围课堂深度拓展•考点一参数方程化为普通方程参数方程化为普通方程的技巧将参数方程化为普通方程,关键是消去参数,常用的消元法有代入消元法、加减消元法.如果参数方程是分式方程,在运用代入消元或加减消元之前做必要的变形.另外,熟悉一些常见的恒等式至关重要,如sin2α+cos2α=1,(ex+e-x)2-(ex-e-x)2=4,1-k21+k22+2k1+k22=1等.【例题1】(2016·华师一附中高三五月质检)将下列参数方程化为普通方程,并说明方程表示的曲线.(1)x=1-3t,y=4t(t为参数);(2)x=1+4cost,y=-2+4sint(t为参数,0≤t≤π);(3)x=2+sin2θ,y=-1+cos2θ(θ为参数);(4)x=sinθ+cosθ,y=sin2θ(θ为参数).•思维导引:把普通方程化成参数方程后,很容易改变变量的取值范围,从而使得两种方程所表示的曲线不一致,因此我们在解题时一定要验证普通方程与参数方程的等价性.解析:(1)由已知t=1-x3,代入y=4t中,得4x+3y-4=0,它就是所求的普通方程,它表示的是一条直线.•(2) 0≤t≤π,-1≤cost≤1,0≤sint≤1.•∴-3≤x≤5,-2≤y≤2,•(x-1)2+(y+2)2=16cos2t+16sin2t=16.•∴(x-1)2+(y+2)2=16(-3≤x≤5,-2≤y≤2),•它表示的曲线是以(1,-2)为圆心,半径为4的上半圆.•(3)由y=-1+cos2θ可得y=-2sin2θ,把sin2θ=x-2代入y=-2sin2θ可得y=-2(x-2),即2x+y-4=0,•又 2≤2+sin2θ≤3,即2≤x≤3,•∴所求的方程是2x+y-4=0(2≤x≤3),它表示的是一条线段.(4)由x=sinθ+cosθ平方得x2=1+2sinθ·cosθ=1+sin2θ,又y=sin2θ代入上式得,x2=1+y,又x=sinθ+cosθ=2sinθ+π4∈[-2,2],...