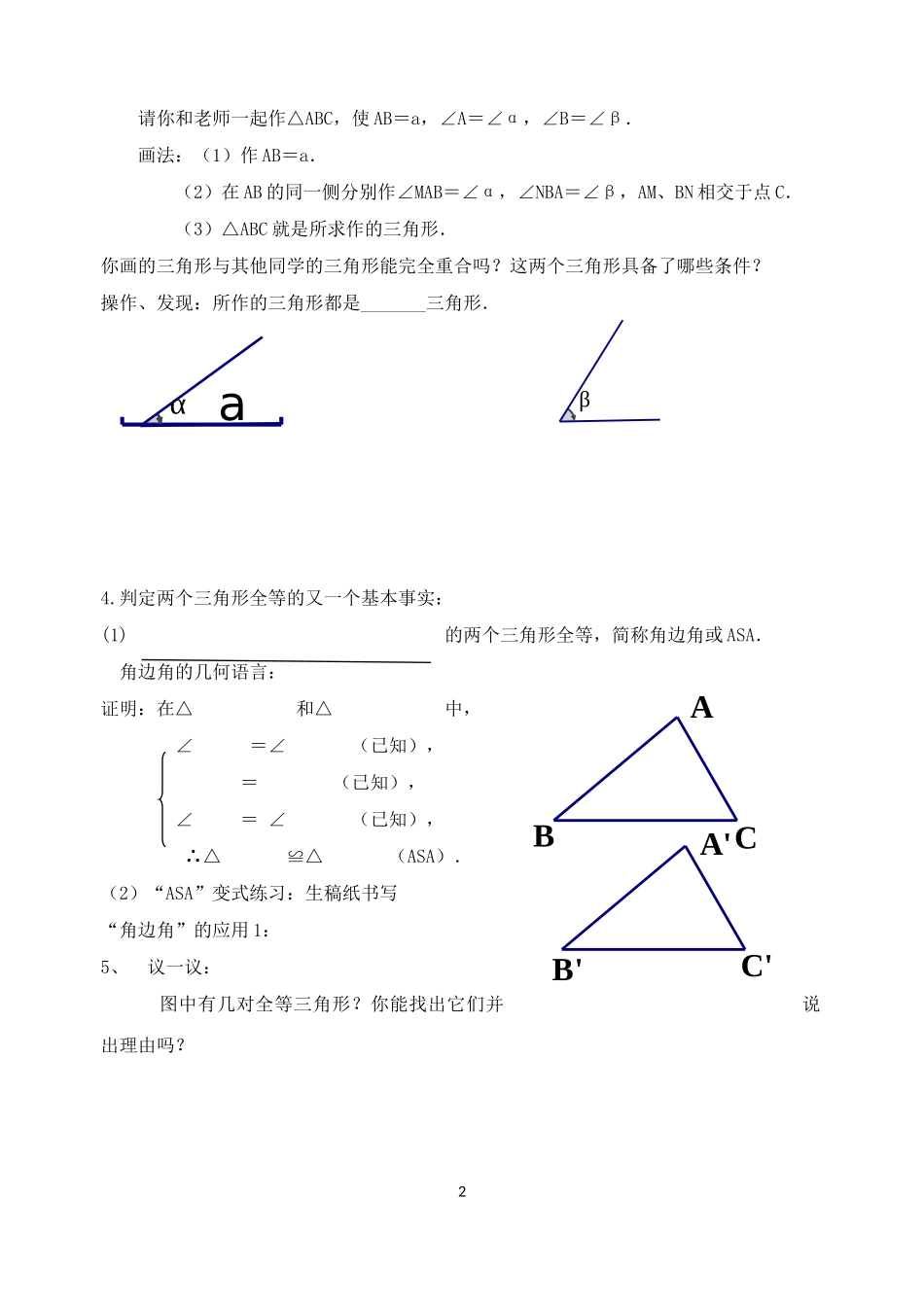
1.3探索三角形全等的条件ASA教学目标:1.经历探索三角形全等“角边角”条件的过程,体会通过操作归纳获得数学结论的过程.2.能运用三角形全等的“角边角”条件,进行有条理的思考和简单的推理。3.进一步学会文字语言、符号语言和图形语言的表达和相互转化.4.通过多种手段的活动过程,让学生动手操作,激发学生学习的兴趣,并能通过合作交流解决问题,体会数学在现实生活中的应用。教学重点:掌握三角形全等的条件“ASA”,并能利用它们判定三角形是否全等教学难点:探索三角形全等的条件“ASA”的过程及应用.教学过程:回顾思考:同学们,经过前面内容的学习,我们了解到:要证明两个三角形全等,只需要几个条件?上节课我们学习了两个三角形只要具备哪三个条件就全等?你能用几何语言描述吗?探索新知一1.先猜,后画老师一个三角形教具不小心撕破了,一个如图(1),一个如图(2),用其中任意一张你能制作一张与原来同样大小的教具吗?试试看。2.说一说:观察下图中的三角形,先猜一猜,哪两个三角形是全等三角形?你能验证吗?3.画一画1(1)(2)A2.5CB60°40°FED2.560°40°2.5PRQ60°40°请你和老师一起作△ABC,使AB=a,∠A=∠α,∠B=∠β.画法:(1)作AB=a.(2)在AB的同一侧分别作∠MAB=∠α,∠NBA=∠β,AM、BN相交于点C.(3)△ABC就是所求作的三角形.你画的三角形与其他同学的三角形能完全重合吗?这两个三角形具备了哪些条件?操作、发现:所作的三角形都是_______三角形.4.判定两个三角形全等的又一个基本事实:(1)的两个三角形全等,简称角边角或ASA.角边角的几何语言:证明:在△和△中,∠=∠(已知),=(已知),∠=∠(已知),∴△≌△(ASA).(2)“ASA”变式练习:生稿纸书写“角边角”的应用1:5、议一议:图中有几对全等三角形?你能找出它们并说出理由吗?2βaαC'B'A'ABC试一试:1、已知:如图,AB、CD相交于点E,∠C=∠D,CE=DE求证:△ADE≌⊿BCE.2.如图,AB,CD相交于点O,O是AB的中点,AC∥BD,求证:O是CD的中点.3、如图,AB=AC还需补充条件____,就可根据“ASA”证明:△ABE≌△ACD.3DECBACEDBA3.已知:如图,∠ABC=∠DCB,∠ACB=∠DBC,求证△ABC≌△DCB6、角边角基本事实的应用:例4.已知:如图,在△ABC中,D是BC的中点,点E、F分别在AB、AC上,且DE//AC,DF//AB.求证:(1)△BDE≌△DCF.(2)BE=DF,DE=CF.7跳一跳:如图,在四边形ABCD中,点E在AC上,∠1=∠2,∠3=...