八年级上册数学苏科版 1.3.3探索三角形全等的条件AAS.docVIP免费

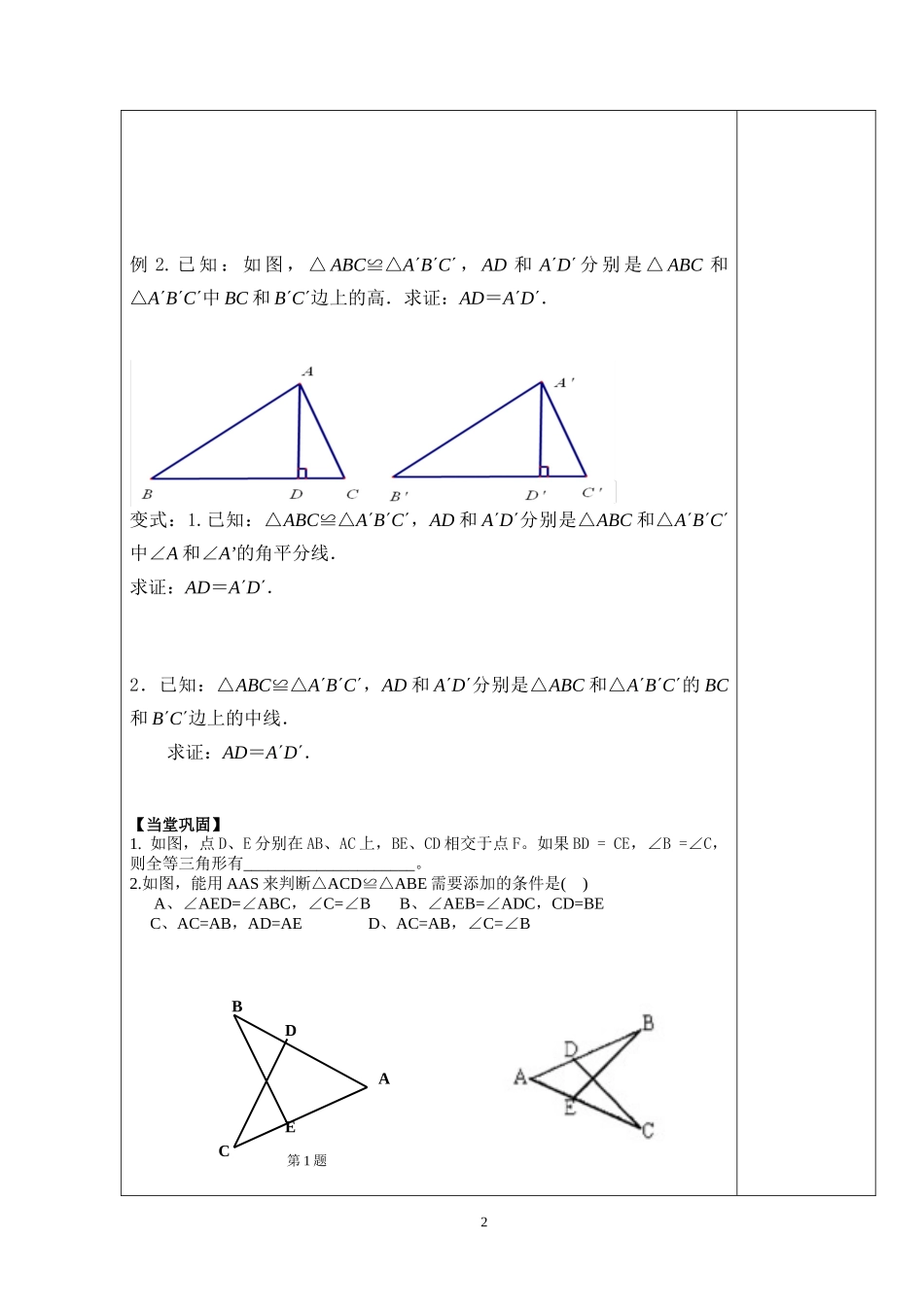
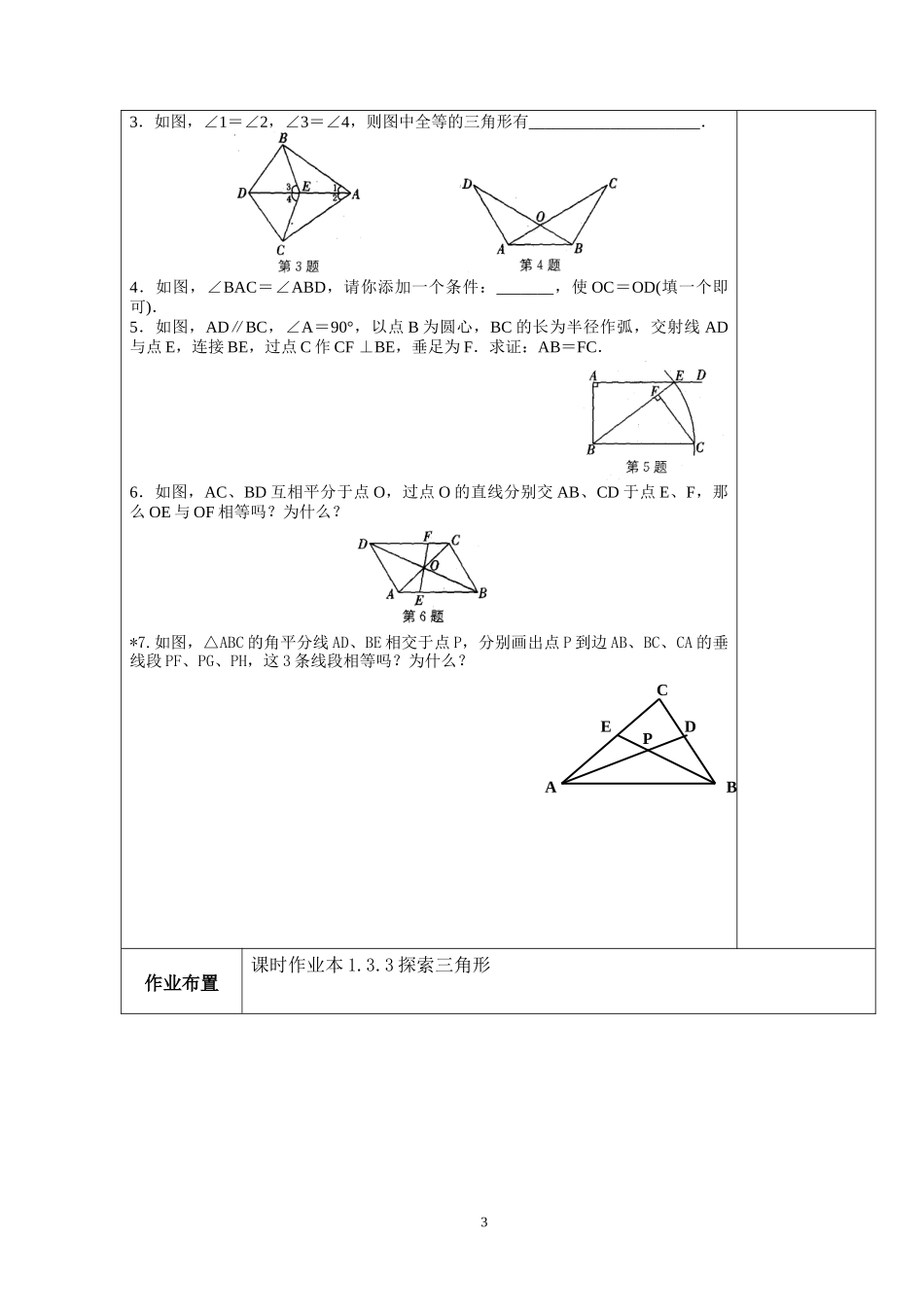
课题探索三角形全等的条件课型新授课教学目标知识目标：1．经历探索三角形全等“角角边”条件的过程，体会通过操作、归纳获得数学结论的过程．2．掌握三角形全等的“角角边”条件，并能运用“角角边”判定两个三角形全等．3．能够进一步结合具体问题和情境进行有条理的思考和简单的推理证明．4．进一步学会文字语言、符号语言和图形语言的表达和相互转化．能力目标：体会通过合情推理探索数学结论，运用演绎推理加以证明的过程，在多种形式的数学活动中，发展合情推理与演绎推理的能力。情感目标：在探索的过程中，感受从特殊到一般、从具体到抽象的思考问题的方法教学重点、难点重点：掌握三角形全等的“角角边”条件难点：能运用“角角边”判定两个三角形全等教学过程设计思路一、新课引入1.复习回顾判定三角形全等的方法：2.探索新知如图，在△ABC和△MNP中，∠A=∠M，∠B=∠N，BC=NP。△ABC与△MNP全等吗？为什么？你能得到什么结论？试着证明。归纳：基本事实（ASA）的推论：练习：1．如图∠ACB＝∠DFE，BC＝EF，根据“ASA”，应补充一个直接条件__________根据“AAS”，那么补充的条件为______，才能使△ABC≌△DEF．2．如图，BE＝CD，∠1＝∠2，则AB＝AC吗？为什么？【例题讲解】例1.如图，点B、E、C、F在同一条直线上，AB＝DE，∠A＝∠D，AC∥DF．求证：(1)△ABC≌△DEF．(2)BE＝CF．1ABCMNP例2.已知：如图，△ABC≌△ABC，AD和AD分别是△ABC和△ABC中BC和BC边上的高．求证：AD＝AD．变式：1.已知：△ABC≌△ABC，AD和AD分别是△ABC和△ABC中∠A和∠A’的角平分线．求证：AD＝AD．2．已知：△ABC≌△ABC，AD和AD分别是△ABC和△ABC的BC和BC边上的中线．求证：AD＝AD．【当堂巩固】1.如图，点D、E分别在AB、AC上，BE、CD相交于点F。如果BD=CE，∠B=∠C，则全等三角形有_____________________。2.如图，能用AAS来判断△ACD≌△ABE需要添加的条件是()A、∠AED=∠ABC，∠C=∠BB、∠AEB=∠ADC，CD=BEC、AC=AB，AD=AED、AC=AB，∠C=∠B2ABCDE第1题第2题3．如图，∠1＝∠2，∠3＝∠4，则图中全等的三角形有_____________________．4．如图，∠BAC＝∠ABD，请你添加一个条件：_______，使OC＝OD(填一个即可)．5．如图，AD∥BC，∠A＝90°，以点B为圆心，BC的长为半径作弧，交射线AD与点E，连接BE，过点C作CF⊥BE，垂足为F．求证：AB＝FC．6．如图，AC、BD互相平分于点O，过点...