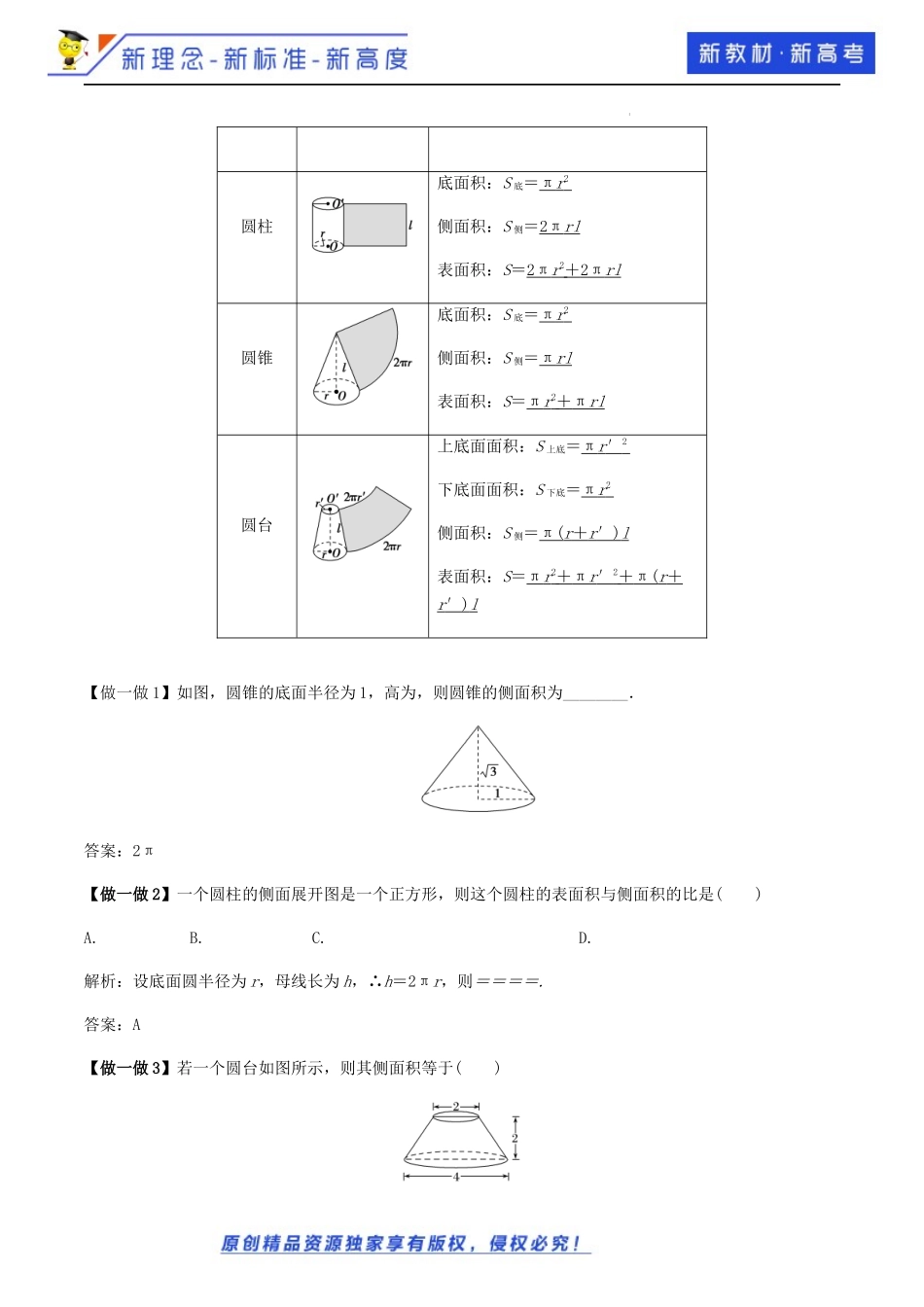
学科网(北京)股份有限公司《8.3简单几何体的表面积和体积》第2课时圆柱、圆锥、圆台、球的表面积和体积教学设计本小节内容选自《普通高中数学必修第二册》人教A版(2019)第八章《立体几何初步》的第三节《简单几何体的表面积和体积》。以下是本节的课时安排:8.3简单几何体的表面积和体积课时内容第1课时棱柱、棱锥、棱台的表面积和体积第2课时圆柱、圆锥、圆台、球的结构特征所在位置教材第114页教材第116页新教材内容分析本节内容是棱柱、棱锥、棱台的表面积与体积求法,由之前学过的正方体、长方体的表面积与体积导入,引出本节要学的内容。本节内容是圆柱、圆锥、圆台与球的表面积与体积求法,由上一节的多面体表面积与体积导入,引出本节要学的内容。核心素养培养借助棱柱、棱锥、棱台的表面积、体积的计算,培养数学运算素养;通过对棱柱、棱锥、棱台的体积的探究,提升逻辑推理的素养.借助圆柱、圆锥、圆台、球的表面积、体积的计算,培养数学运算素养;通过对圆柱、圆锥、圆台、球的体积的探究,提升逻辑推理的素养.教学主线圆柱、圆锥、圆台、球的结构前面我们明确研究对象:棱柱、棱锥、棱台的结构特征,为本节学习圆柱、圆锥、圆台的表面积和体积做好知识准备.学科网(北京)股份有限公司1.了解圆柱、圆锥、圆台、球的表面积和体积的计算公式,培养数学抽象的核心素养;2.理解并掌握侧面展开图与几何体的表面积之间的关系,并能利用计算公式求几何体的表面积与体积,提升数学运算的核心素养。1.重点:通过对圆柱、圆锥、圆台的研究,掌握圆柱、圆锥、圆台、球的表面积与体积的求法。2.难点:会求与圆柱、圆锥、圆台、球有关的组合体的表面积与体积。(一)新知导入1.创设情境,生成问题如图是工厂生产的各种金属零件,被广泛应用于工业领域的各个方面.【问题】(1)如果已知制作零件的金属的密度,如何求出这些零件的质量?(2)如图所示的零件都是旋转体,其侧面都是曲面,如何求其表面积?【提示】(1)先求出金属零件的体积,再求其质量.(2)求其侧面展开图的面积,再加上底面面积就是其表面积.(二)圆柱、圆锥、圆台、球的表面积和体积知识点一圆柱、圆锥、圆台的表面积旋转体侧面展开图底面积、侧面积、表面积学科网(北京)股份有限公司圆柱底面积:S底=πr2侧面积:S侧=2πrl表面积:S=2πr2+2πrl圆锥底面积:S底=πr2侧面积:S侧=πrl表面积:S=πr2+πrl圆台上底面面积:S上底=πr′2下底面面积:S下底=πr2侧面积:S侧...