第5课时 相似三角形的判定.pptVIP免费

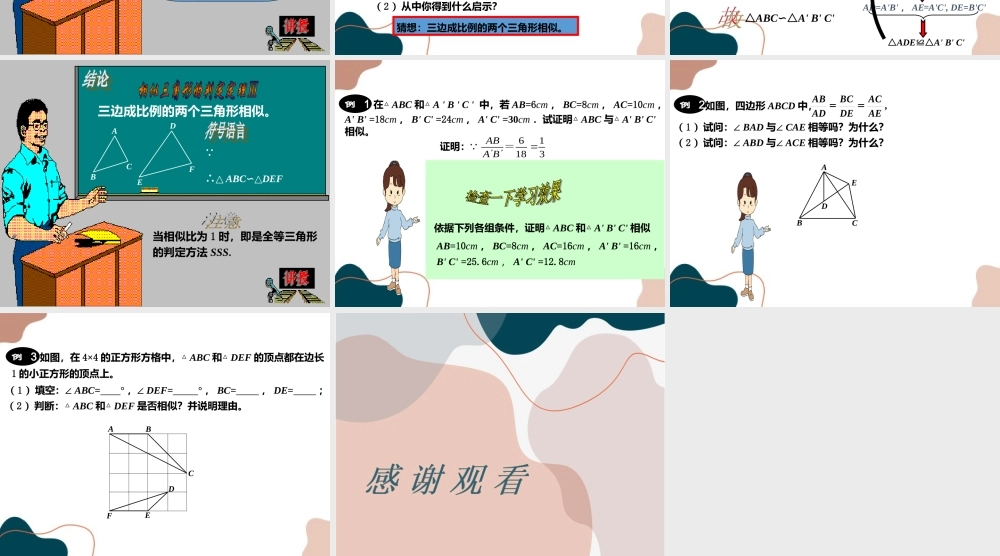
第23章图形的相似23.3相似三角形第5课时相似三角形的判定定理3长长中中短短相似三角形的对应边成比例，对应角相等。ABCFDE∵△ABC∽△DEF∴∠A=∠D∠B=∠E∠C=∠FDFACEFBCDEAB平行于三角形一边的直线，和其他两边（或两边的延长线）相交所构成的三角形和原三角形相似。∵DE//BCBCADEABCDE∴△ADE∽△ABC“A”型“X”型这是我们以后经常研究的两种基本图形。两角分别相等的两个三角形相似。ABCFDE∵∠A=∠D，∠B=∠E∴△ABC∽△DEFDADFACDEAB，两边成比例且夹角相等的两个三角形相似。ABCFDE∵∴△ABC∽△DEF角一定是两边的夹角哟！是否还有另外的方法呢？在下图的方格上任画一个三角形，再画出第二个三角形，使它的三边长都是原来三角形的三边长的相同倍数．（1）画完之后，用量角器比较两个三角形的对应角，你发现了什么结论？大家的结论都一样吗？ABCA'B'C'（2）从中你得到什么启示？猜想：三边成比例的两个三角形相似。A'B'C'ACBDE如图，在△ABC和△A'B'C'中，.求证：△ABC∽△A'B'C'CBBCCAACBAAB在边AB上截取AD=A'B'，过点D作DE//BC交AC于点EDE//BC△ADE∽△ABCDEBCAEACADABCBBCCAACBAABAD=A'B'AD=A'B'，AE=A'C',DE=B'C'△ADE≌△A'B'C'△ABC∽△A'B'C'从中得到什么感悟？三边成比例的两个三角形相似。EFBCDFACDEAB三边成比例的两个三角形相似。ABCFDE∵∴△ABC∽△DEF当相似比为1时，即是全等三角形的判定方法SSS.例1在△ABC和△A'B'C'中，若AB=6cm，BC=8cm，AC=10cm，A'B'=18cm，B'C'=24cm，A'C'=30cm．试证明△ABC与△A'B'C'相似。31＝248＝CBBC31186＝BAAB证明：∵CBBCCAACBAAB∴31＝3010＝CAAC∴△ABC∽△A'B'C'依据下列各组条件，证明△ABC和△A'B'C'相似AB=10cm，BC=8cm，AC=16cm，A'B'=16cm，B'C'=25.6cm，A'C'=12.8cmEABCD如图，四边形ABCD中，例2==,ABBCACADDEAE（1）试问：∠BAD与∠CAE相等吗？为什么？（2）试问：∠ABD与∠ACE相等吗？为什么？例3如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长（2）判断：△ABC和△DEF是否相似？并说明理由。（1）填空：∠ABC=°，∠DEF=°，BC=，DE=；1的小正方形的顶点上。CAEBFD