第4课时 相似三角形的判定.pptVIP免费

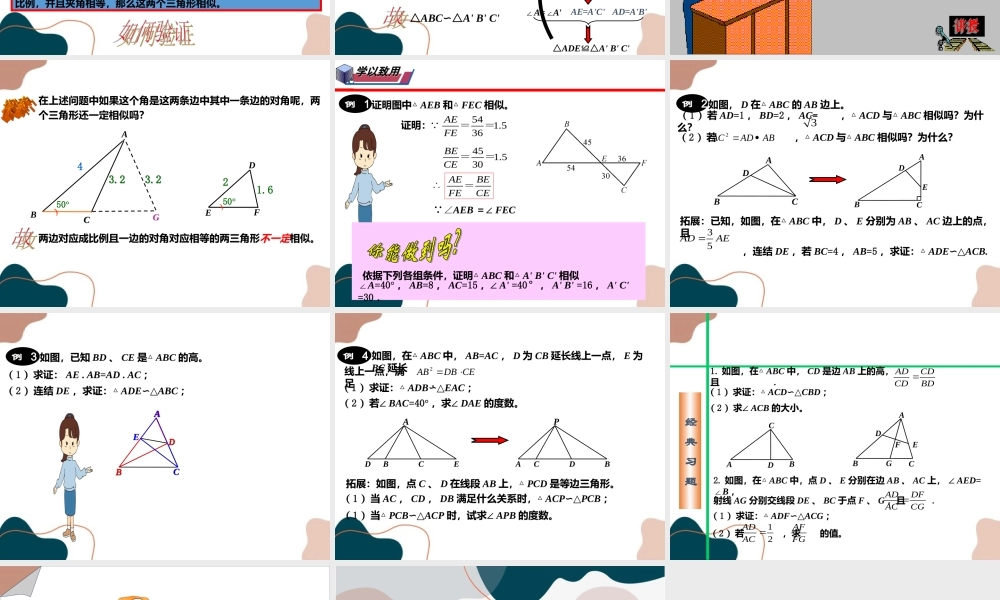
第23章图形的相似23.3相似三角形第4课时相似三角形的判定定理2长长中中短短相似三角形的对应边成比例，对应角相等。ABCFDE △ABC∽△DEF∴∠A=∠D∠B=∠E∠C=∠FDFACEFBCDEAB平行于三角形一边的直线，和其他两边（或两边的延长线）相交所构成的三角形和原三角形相似。 DE//BCBCADEABCDE∴△ADE∽△ABC“A”型“X”型这是我们以后经常研究的两种基本图形。两角分别相等的两个三角形相似。ABCFDE ∠A=∠D，∠B=∠E∴△ABC∽△DEF是否还有另外的方法呢？观察下图，如果有一点E在边AC上，那么点E应该在什么位置才能使△ADE与△ABC相似呢？ABCDE图中△ADE与△ABC的一组对应边AD与AB的长度的比值为,将点E由点A开始在AC上移动,31发现当AE=AC时，△ADE与△ABC相似.此时ABAD=____．31ACAE类比猜想：如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。类比猜想:我们在判断两个三角形全等时，使用了哪些方法？判断三角形相似是否有类似的方法呢？A'B'C'ACBDE如图，在△ABC和△A'B'C'中，∠A=∠A'，.求证：△ABC∽△A'B'C'CAACBAAB在边AB上截取AD=A'B'，过点D作DE//BC交AC于点EDE//BC△ADE∽△ABCAEACADABCAACBAABAD=A'B'AE=A'C'∠A=∠A'AD=A'B'△ADE≌△A'B'C'△ABC∽△A'B'C'从中得到什么感悟？两边成比例且夹角相等的两个三角形相似。DADFACDEAB，两边成比例且夹角相等的两个三角形相似。ABCFDE ∴△ABC∽△DEF角一定是两边的夹角哟！在上述问题中如果这个角是这两条边中其中一条边的对角呢，两个三角形还一定相似吗？GG3.23.2CC3.23.250°)4AB21.650°)EDF两边对应成比例且一边的对角对应相等的两三角形不一定相似。两边对应成比例且一边的对角对应相等的两三角形不一定相似。学以致用学以致用例1证明图中△AEB和△FEC相似。5.1＝3045＝CEBE5.1＝3654＝FEAE证明： CEBEFEAE＝∴∴△AEB∽△FEC ∠AEB＝∠FEC依据下列各组条件，证明△ABC和△A'B'C'相似∠A=40°，AB=8，AC=15，∠A'=40°，A'B'=16，A'C'=30．例2如图，D在△ABC的AB边上。3（1）若AD=1，BD=2，AC=，△ACD与△ABC相似吗？为什么？ABCD（2）若，△ACD与△ABC相似吗？为什么？ABADAC2拓展：已知，如图，在△ABC中，D、E分别为AB、AC边上的点，且，连结DE，若BC=4，AB=5，求证：△ADE∽△ACB.AEAD53EDABC例3如图，已知BD、CE是△ABC的高。（2）连结DE，求证：△ADE∽△ABC；（1）求证：AE.AB=AD.A...