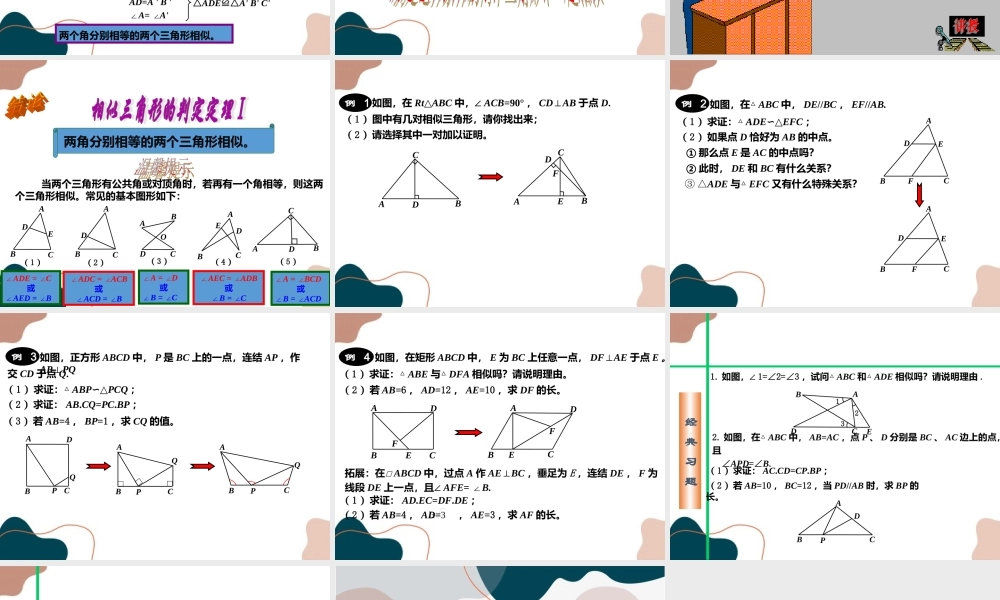
第23章图形的相似23.3相似三角形第3课时相似三角形的判定定理1长长中中短短相似三角形的对应边成比例,对应角相等。ABCFDE △ABC∽△DEF∴∠A=∠D∠B=∠E∠C=∠FDFACEFBCDEAB平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形和原三角形相似。 DE//BCBCADEABCDE∴△ADE∽△ABC“A”型“X”型这是我们以后经常研究的两种基本图形。如图是两个含30°锐角的直角三角形,它们相似吗?ABCA'B'C'ACBA'B'C'猜想:如果两个三角形的三个角分别相等,那么这两个三角形相似。A'B'C'如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B'.ACBA'B'C'从中得到什么感悟?DEDE//BC△ADE∽△ABC∠ADE=∠BAD=A'B'∠A=∠A'△ADE≌△A'B'C'△ABC∽△A'B'C'两个角分别相等的两个三角形相似。试问:△ABC和△A'B'C'相似吗?如图,在△ABC和△A'B'C'中,∠A=∠A'.试问:△ABC和△A'B'C'相似吗?A'B'C'ABC两角分别相等的两个三角形相似。ABCFDE ∠A=∠D,∠B=∠E∴△ABC∽△DEF两角分别相等的两个三角形相似。当两个三角形有公共角或对顶角时,若再有一个角相等,则这两个三角形相似。常见的基本图形如下:EDABC(1)DABC(2)ODABC(3)DEABC(4)∠ADE=∠C或∠AED=∠B∠ADC=∠ACB或∠ACD=∠B∠A=∠D或∠B=∠C∠AEC=∠ADB或∠B=∠C∠A=∠BCD或∠B=∠ACDDABC(5)例1如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.DABCEFDABC(1)图中有几对相似三角形,请你找出来;(2)请选择其中一对加以证明。例2如图,在△ABC中,DE//BC,EF//AB.(1)求证:△ADE∽△EFC;(2)如果点D恰好为AB的中点。①那么点E是AC的中点吗?②此时,DE和BC有什么关系?③△ADE与△EFC又有什么特殊关系?ABCDEFABCDEF例3如图,正方形ABCD中,P是BC上的一点,连结AP,作AP⊥PQ交CD于点Q.(1)求证:△ABP∽△PCQ;(2)求证:AB.CQ=PC.BP;(3)若AB=4,BP=1,求CQ的值。QPDABCQPABCQPABC例4如图,在矩形ABCD中,E为BC上任意一点,DF⊥AE于点E。(1)求证:△ABE与△DFA相似吗?请说明理由。(2)若AB=6,AD=12,AE=10,求DF的长。EABCDF拓展:在□ABCD中,过点A作AE⊥BC,垂足为E,连结DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:AD.EC=DF.DE;(2)若AB=4,AD=,AE=3,求AF的长。33CABDEF经典习题1.如图,∠1=∠2=∠3,试问△ABC和△ADE相似吗?请说明理由.CDEBA1232.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.(1)求证:AC.CD=CP.BP;(2...