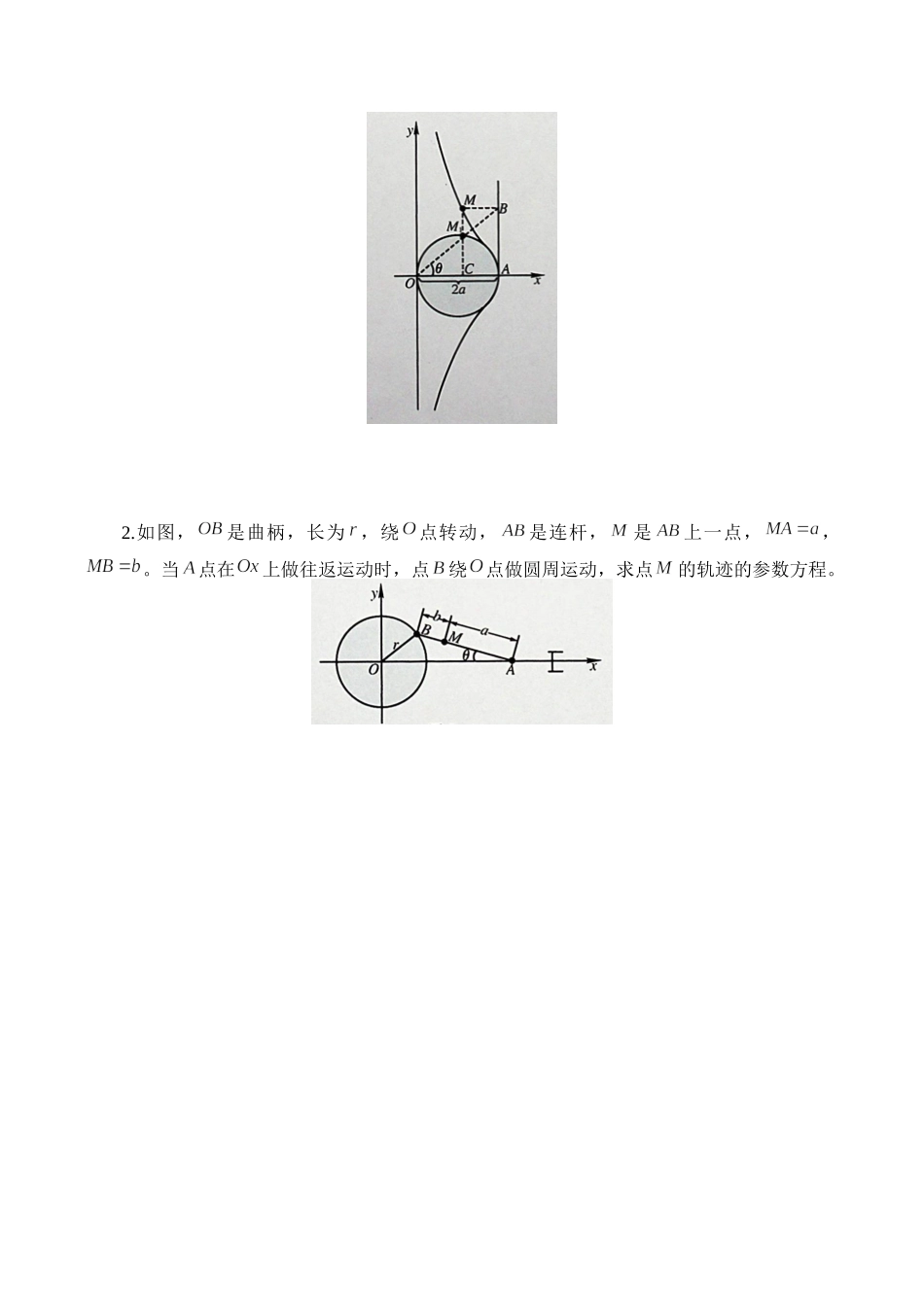
渐开线及其参数方程【学习目标】1.掌握渐开线的相关知识。2.熟练运用渐开线的参数方程解决一些具体问题。3.亲历渐开线的参数方程推导的探究过程,得到渐开线的参数方程结论,提高发现问题、思考问题、解决问题。【学习重难点】重点:理解并掌握渐开线的参数方程推导的步骤。难点:渐开线的参数方程的实际应用。【学习过程】一、新课学习知识点一:渐开线的定义在一个固定的圆盘上的圆周上缠绕着一条无弹性的柔顺细线,在此细线的外端系上一支铅笔,把此线拉紧保持与此圆相切地逐渐展开,铅笔画出的曲线称为此圆的渐开线。知识点二:圆渐开线的参数方程为同学们自行进行该参数方程的推导:知识点三:由渐开线定义,关于同一个基圆,存在两条渐开线,两者关于轴对称。三、课程总结1.这节课我们主要学习了哪些知识?(1)渐开线的定义;(2)圆的渐开线的参数方程;(3)由渐开线定义,关于同一个基圆,存在两条渐开线,两者关于轴对称。2.它们在解题中具体怎么应用?四、习题检测1.如图,是定圆直径,长,直线与圆交于,和过点的切线交于,,平行于,与交于,以为原点,为轴正半轴,求动点轨迹的参数方程。2.如图,是曲柄,长为,绕点转动,是连杆,是上一点,,。当点在上做往返运动时,点绕点做圆周运动,求点的轨迹的参数方程。