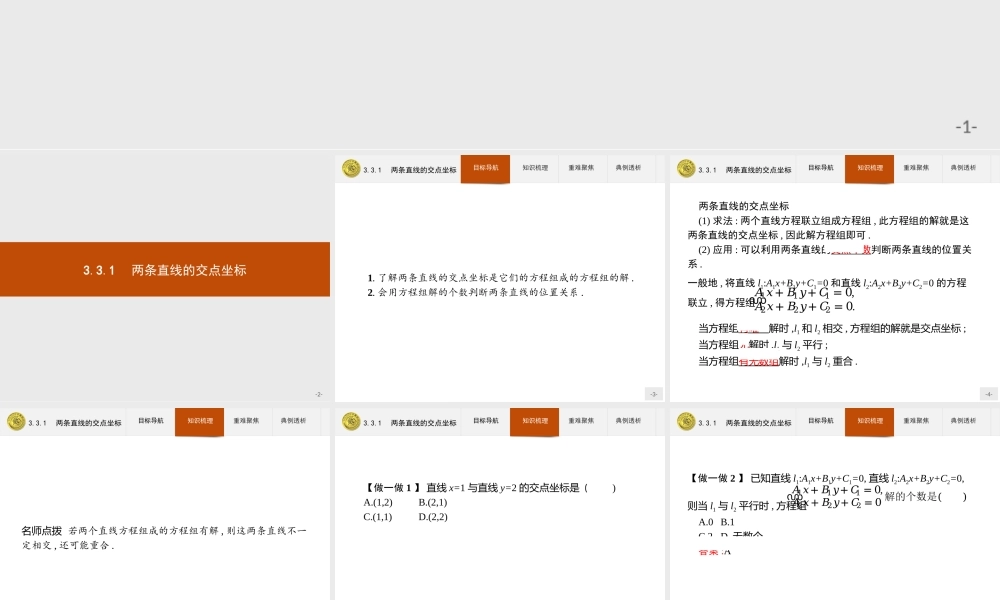
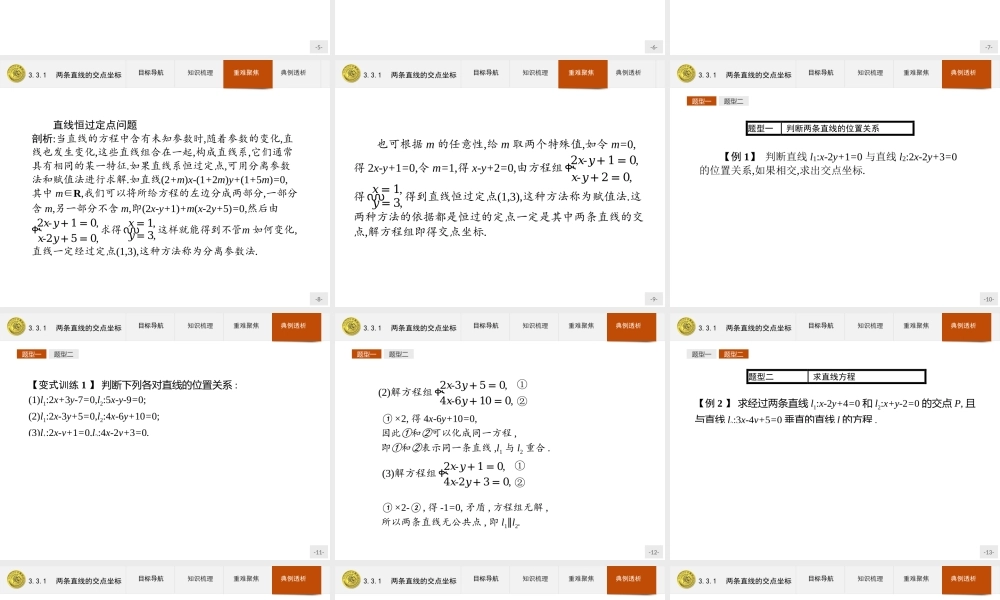
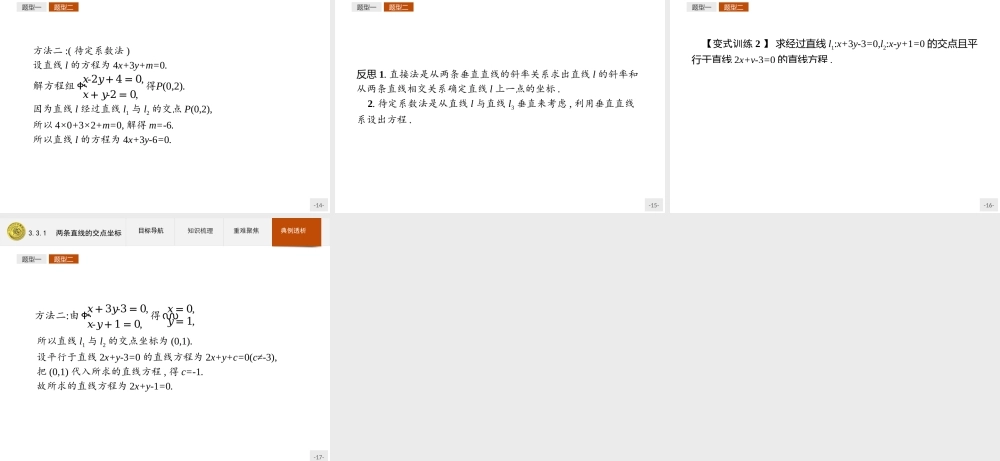
-1-3.3直线的交点坐标与距离公式-2-3.3.1两条直线的交点坐标-3-3.3.1两条直线的交点坐标目标导航知识梳理重难聚焦典例透析1.了解两条直线的交点坐标是它们的方程组成的方程组的解.2.会用方程组解的个数判断两条直线的位置关系.-4-3.3.1两条直线的交点坐标目标导航知识梳理重难聚焦典例透析两条直线的交点坐标(1)求法:两个直线方程联立组成方程组,此方程组的解就是这两条直线的交点坐标,因此解方程组即可.(2)应用:可以利用两条直线的交点个数判断两条直线的位置关系.一般地,将直线l1:A1x+B1y+C1=0和直线l2:A2x+B2y+C2=0的方程联立,得方程组൜𝐴1𝑥+𝐵1𝑦+𝐶1=0,𝐴2𝑥+𝐵2𝑦+𝐶2=0.当方程组有唯一解时,l1和l2相交,方程组的解就是交点坐标;当方程组无解时,l1与l2平行;当方程组有无数组解时,l1与l2重合.-5-3.3.1两条直线的交点坐标目标导航知识梳理重难聚焦典例透析名师点拨若两个直线方程组成的方程组有解,则这两条直线不一定相交,还可能重合.-6-3.3.1两条直线的交点坐标目标导航知识梳理重难聚焦典例透析【做一做1】直线x=1与直线y=2的交点坐标是()A.(1,2)B.(2,1)C.(1,1)D.(2,2)答案:A-7-3.3.1两条直线的交点坐标目标导航知识梳理重难聚焦典例透析【做一做2】已知直线l1:A1x+B1y+C1=0,直线l2:A2x+B2y+C2=0,则当l1与l2平行时,方程组A.0B.1C.2D.无数个答案:A൜𝐴1𝑥+𝐵1𝑦+𝐶1=0,𝐴2𝑥+𝐵2𝑦+𝐶2=0解的个数是()-8-3.3.1两条直线的交点坐标目标导航知识梳理重难聚焦典例透析直线恒过定点问题剖析:当直线的方程中含有未知参数时,随着参数的变化,直线也发生变化,这些直线组合在一起,构成直线系,它们通常具有相同的某一特征.如果直线系恒过定点,可用分离参数法和赋值法进行求解.如直线(2+m)x-(1+2m)y+(1+5m)=0,其中m∈R,我们可以将所给方程的左边分成两部分,一部分含m,另一部分不含m,即(2x-y+1)+m(x-2y+5)=0,然后由ቊ2𝑥-𝑦+1=0,𝑥-2𝑦+5=0,求得൜𝑥=1,𝑦=3,这样就能得到不管m如何变化,直线一定经过定点(1,3),这种方法称为分离参数法.-9-3.3.1两条直线的交点坐标目标导航知识梳理重难聚焦典例透析也可根据m的任意性,给m取两个特殊值,如令m=0,得2x-y+1=0,令m=1,得x-y+2=0,由方程组ቊ2𝑥-𝑦+1=0,𝑥-𝑦+2=0,得൜𝑥=1,𝑦=3,得到直线恒过定点(1,3),这种方法称为赋值法.这两种方法的依据都是恒过的定点一定是其中两条直线的交点,解方程组即得交点坐标.-10-3.3.1两条直线的交点坐标目标导航知识梳理重难聚焦典例透析题型一题型二题型一判断两条直线的位置关系【例1...