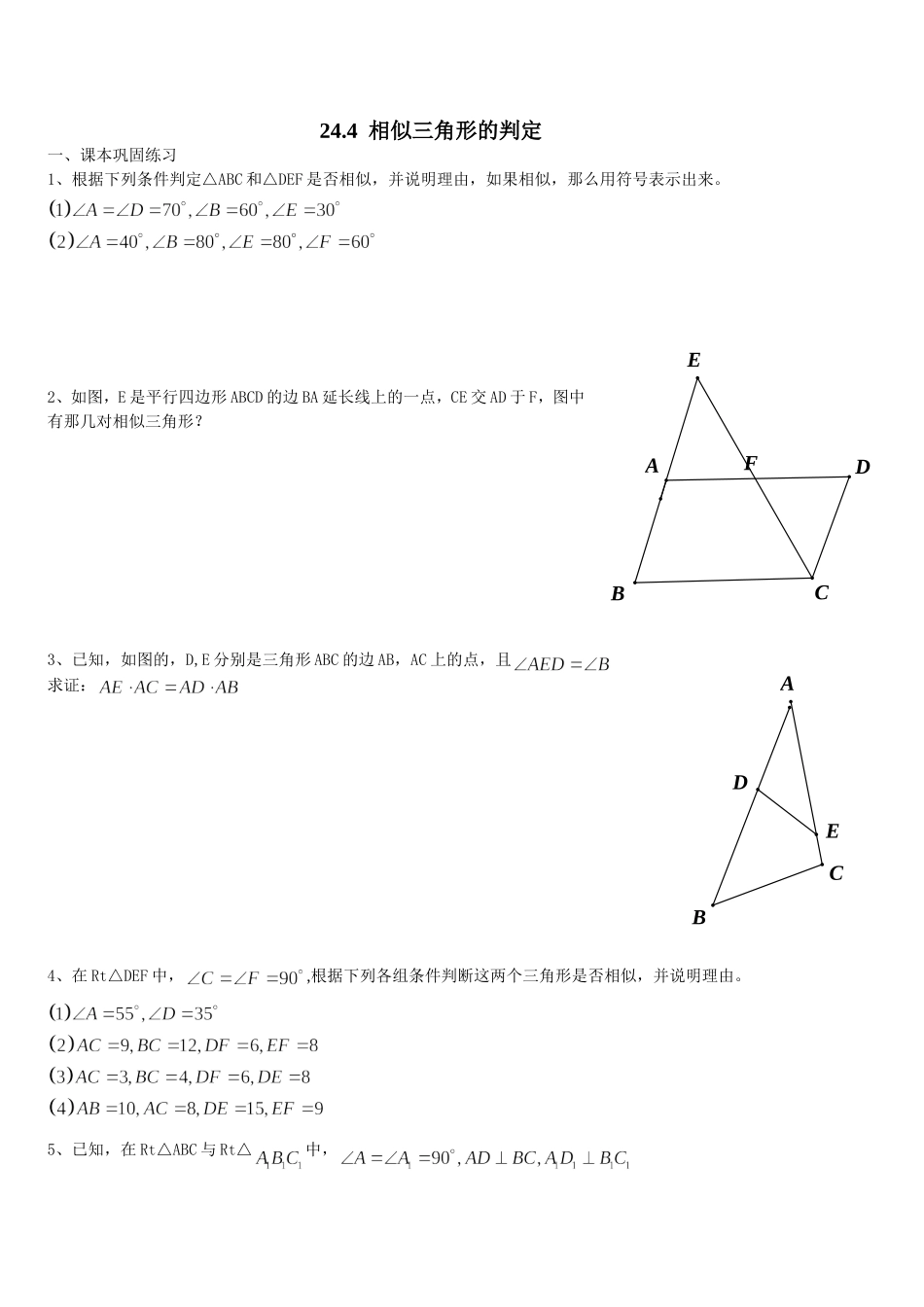
24.4相似三角形的判定一、课本巩固练习1、根据下列条件判定△ABC和△DEF是否相似,并说明理由,如果相似,那么用符号表示出来。2、如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于F,图中有那几对相似三角形?3、已知,如图的,D,E分别是三角形ABC的边AB,AC上的点,且求证:4、在Rt△DEF中,,根据下列各组条件判断这两个三角形是否相似,并说明理由。5、已知,在Rt△ABC与Rt△中,FADBCEBACDE垂足分别为点,且,求证:△ABC∽△二、基础过关1.下列各组的两个图形,一定相似的是()(A)两条对角线分别对应成比例的两个平行四边形(B)等腰梯形的中位线把它分成的两个等腰梯形(C)有一个角对应相等的两个菱形(D)对应边成比例的两个多边形2.M在AB上,且MB=4,AB=12,AC=16,在AC上有一定N,使△AMN与原三角形相似,则AN的长为3.如图,已知D,E分别在△ABC的AB,AC边上,△ABC与△ADE,则下列各式成立的是()(A)=(B)=(C)AD·DE=AE·EC(D)AB·AD=AE·AC4.如图,∠1=∠2,AB·AC=AD·AE,则∠C=.5.如图,△ABC内接正方形DEFG,AM⊥BC于M,交DG于H,若AH长4cm,正方形边长6cm,则BC=.6.如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,求证:△AFE∽△ABC。ADCEBADCEB12ACFEBDGHMACFEB7.如图,平行四边形ABCD中,E是CB延长线上一点,DE交AB于F,求证:AD·AB=AF·CE。9.在△ABC中,AB=AC,∠A=36°,∠ABC的平分线BD与AC交于D,求证:(1)BC=AD(2)△ABC∽△BDC(3)BC=(–1)AB10.如图,已知BD和CE是△ABC的高,∠BAC的平分线交BC于F,交DE于G,求证:BF·EG=CF·DG.11.如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证:(1)=(2)=(3)CE=BM12.如图,△ABC的∠A的内角平分线交BC于P,∠BAC的外角平分线交BC的延长线于Q,M为PQ的中点,求证:(1)MA2=MB·MC(2)=ACFEBDACBDACFEBDGACFEBDMACBMPQ13.如图,已知梯形ABCD中,AD∥BC,AC,BD交于E,过E作FG∥BC,求证:EF=EG.ACFEBDG