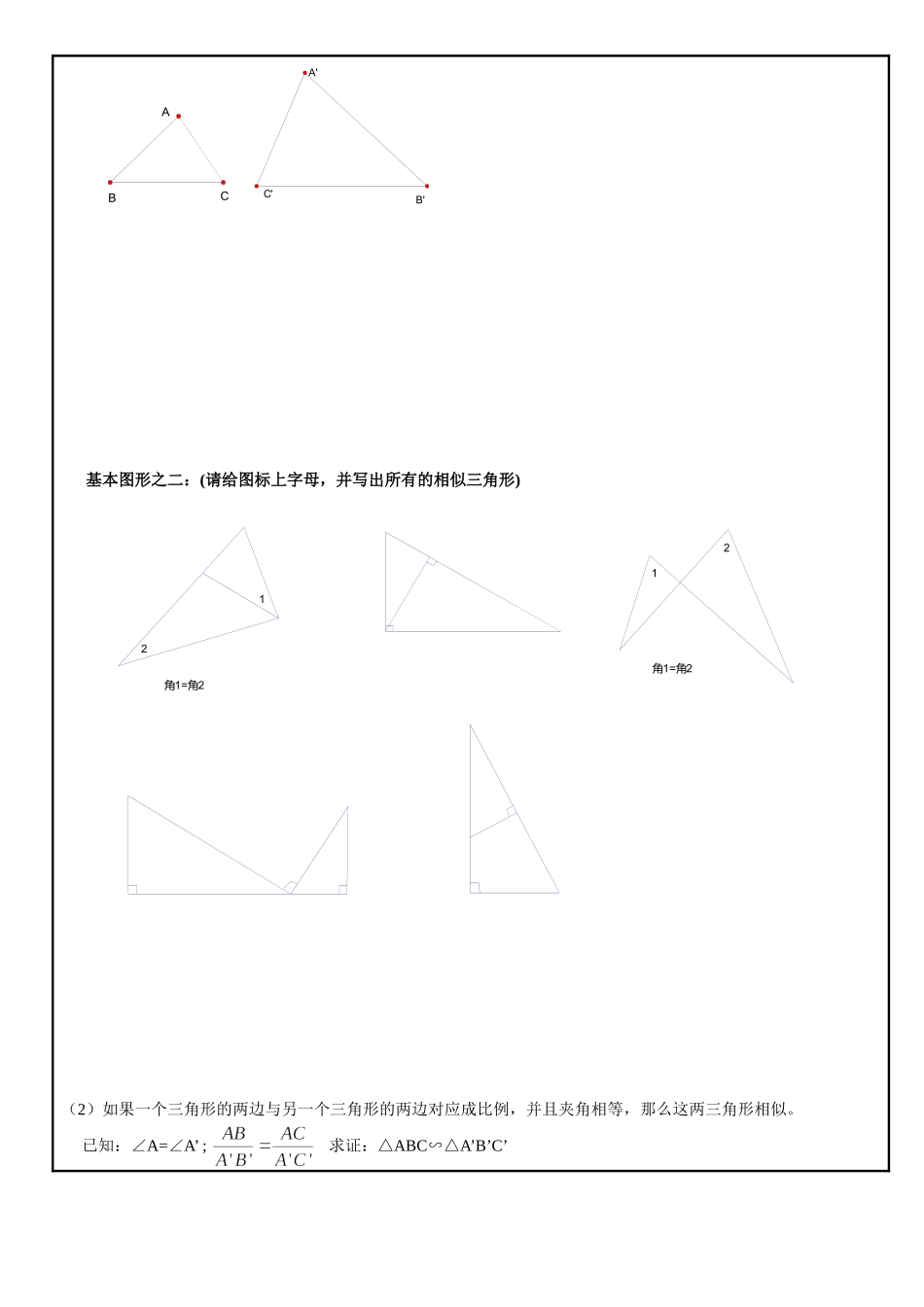
学生编号学生姓名授课教师辅导学科数学所属年级新九年级教材版本沪教版课题名称相似三角形的判定课时进度授课时间月日教学目标相似三角形判定重点难点相似三角形判定知识精要一、相似三角形的概念一个三角形的三个角与另一个三角形的三个角对应相等,且它们各有的三条边对应成比例,那么这两个三角形相似。对应边的比值叫做相似比。即△ABC∽△DEF,我们可以得到:【注意事项1、2、】相似具有连贯性:即两个三角形分别与第三个三角形相似,那么这两个三角形也相似。相似三角形的预备定理:平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似。(∥)【请用所上节课所学习的知识+定义证明】EDCBA基本图形之一:(请添加条件,使之相似)2、判定定理:(1)如果一个三角形的两角与另一个三角形的两角对应相等,那么这两三角形相似。已知:∠A=∠A’;∠B=∠B’求证:△ABC∽△A’B’C’CBAC'B'A'基本图形之二:(请给图标上字母,并写出所有的相似三角形)角1=角221角1=角221(2)如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两三角形相似。已知:∠A=∠A’;求证:△ABC∽△A’B’C’CBAC'B'A'基本图形之三:(请给图标上字母及条件,并写出所有的相似三角形)(3)如果一个三角形的三边与另外一个三角形的三边对应成比例,那么这两三角形相似。(4)直角三角形相似的判定定理:如果一个直角三角形的斜边及一条直角边与另一个三角形的斜边及直角边对应成比例,那么这两直角三角形相似。(HL)【自己画图,写出已知、求证,并证明】【对比】判定条件全等相似(1)(2)(3)(4)直角三角形二、相似三角形的性质1、性质一:相似三角形对应角相等,对应边成比例相似三角形对应高的比,对应中线的比,对应角平分线的比及周长比都等于相似比。【要求自行证明】、【总结】2、性质二:相似三角形的面积的比等于相似比的平方【自行证明】热身练习1、下列条件中,不能判断与相似的是()A.∠A=50°,∠B=70°,∠D=50°,∠F=70°B.,∠B=40°,,∠E=40°C.D.∠A=50°,,∠E=50°2、下列命题正确的是()A.有一个角是40°的两个等腰三角形B.有一个角是100°的两个等腰三角形C.面积相等的两个直角三角形D.两边之比为3:5的两个直角三角形3、如图:△ABC中,∠ACB=90°,CD⊥AB,垂足为D,且,求:(1)CD的长(2)CBDA4、如图:D是△ABC的AB边上一个动点,DE∥BC交AC于E,DF∥AC交BC于F,已知AD:DB=1:2,求三角...