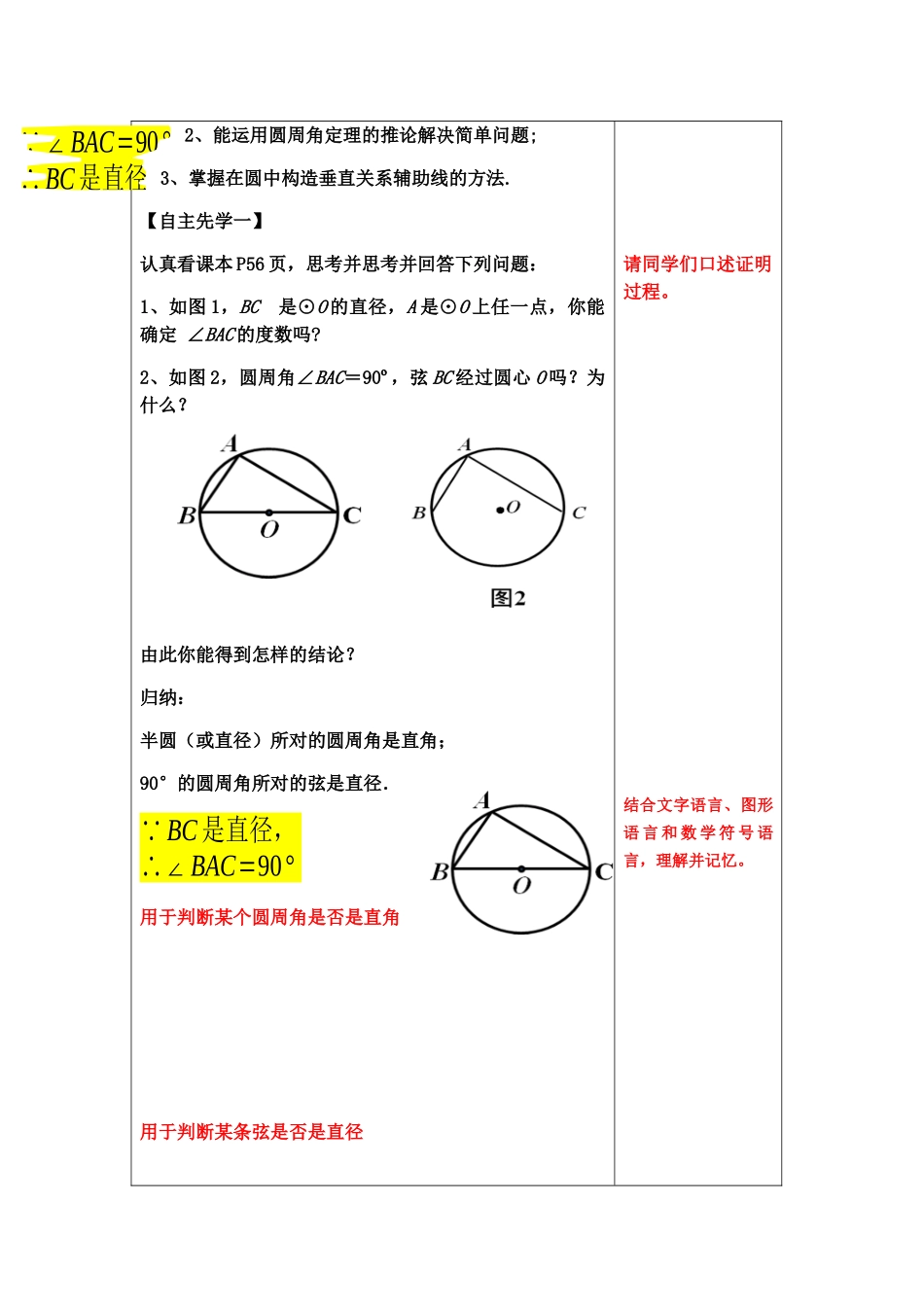
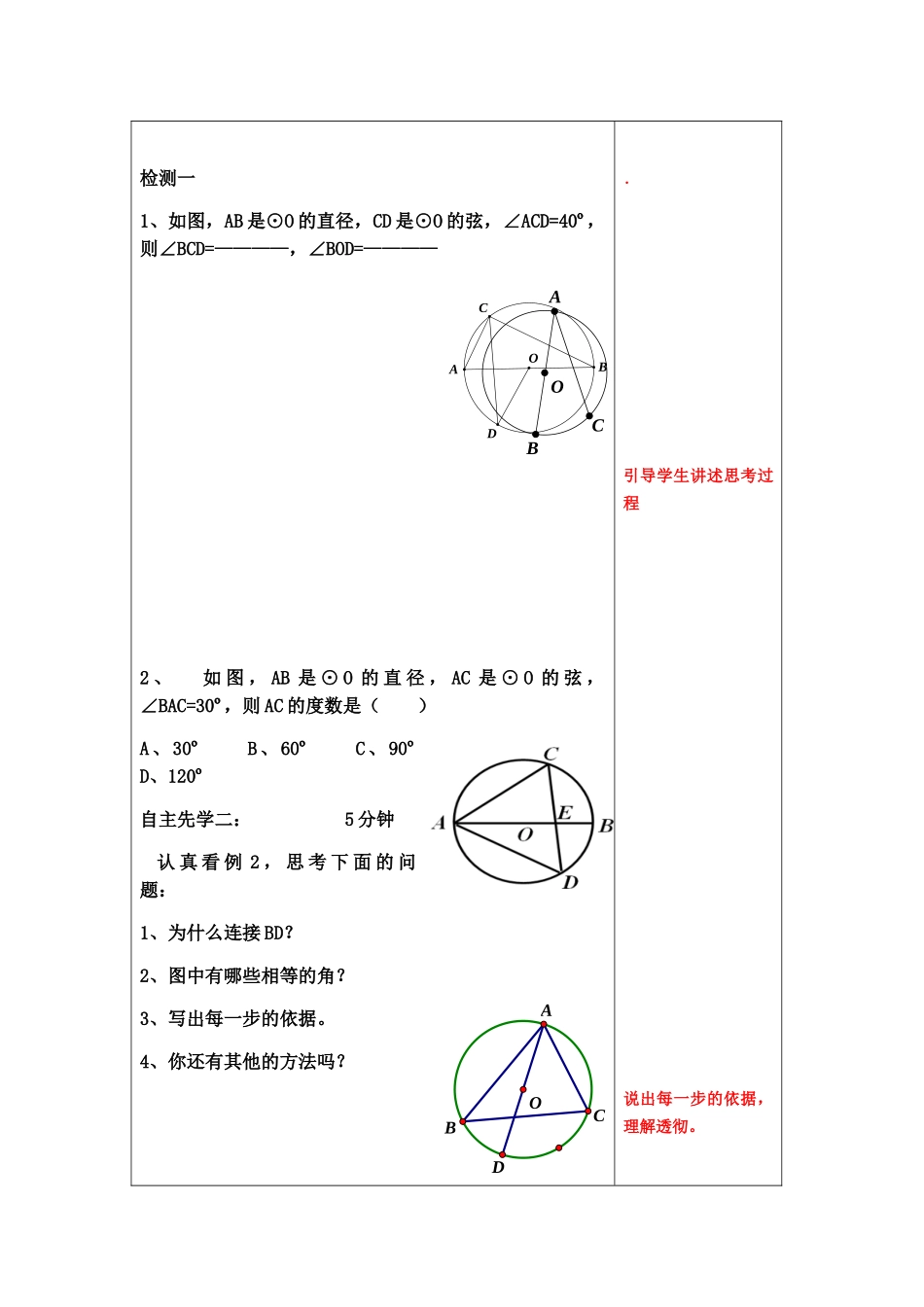
课题2.4圆周角主备主核使用者课型新授课使用日期【学习目标】1、了解并证明圆周角定理的推论;2、能运用圆周角定理的推论解决简单问题;3、掌握在圆中构造垂直关系辅助线的方法.第一次集体备课(通案)第二次备课(个案)【复习回顾】如图,点A、B、C、D在⊙O上,点A与点D在点B、C所在直线的同侧,∠A=35°.(1)∠D=_____°,理由是_______________________;(2)BOC∠=_____°,理由是_____________________________【板书课题】2.4圆周角(2)【学习目标】1、了解并证明圆周角定理的推论;1、每人一个圆形纸片,你能找到圆心吗?2、展示一个圆形模具,你还能找到圆心吗?2、能运用圆周角定理的推论解决简单问题;3、掌握在圆中构造垂直关系辅助线的方法.【自主先学一】认真看课本P56页,思考并思考并回答下列问题:1、如图1,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?2、如图2,圆周角∠BAC=90º,弦BC经过圆心O吗?为什么?由此你能得到怎样的结论?归纳:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径. BC是直径,∴∠BAC=90°用于判断某个圆周角是否是直角用于判断某条弦是否是直径请同学们口述证明过程。结合文字语言、图形语言和数学符号语言,理解并记忆。 ∠BAC=90°∴BC是直径OBACDOCABOADBC检测一1、如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=40º,则∠BCD=————,∠BOD=————2、如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC=30º,则AC的度数是()A、30ºB、60ºC、90ºD、120º自主先学二:5分钟认真看例2,思考下面的问题:1、为什么连接BD?2、图中有哪些相等的角?3、写出每一步的依据。4、你还有其他的方法吗?.引导学生讲述思考过程说出每一步的依据,理解透彻。G检测二:如图,⊙O是ΔABC的外接圆,直径AD=4,∠ABC=∠DAC,求AC的长。拓展延学:小组合作完成已知:BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,AE=AB,BE交AD于点F.判断△FAB的形状,并说明理由.拓展:点F是BG的中点吗?在例3中,若点E与解:连接DC, AD是直径,∴∠ADC=90° ∠ABC=∠DAC,∠ABC=∠ADC,∴∠ADC=∠DAC,∴DC=AC,∴由勾股定理得AC=2√2.OEBACD.,,//.:BEBDBOEDEODOECABCECOECOEOCOE,,连接法二.,,//.90:BEBDDEABABCEDECDCDE是直径,连接法一【课堂小结】这节课你有哪些收获?1、知识性目标:半圆(或直径)所对的圆周角是直角;90°的圆周...