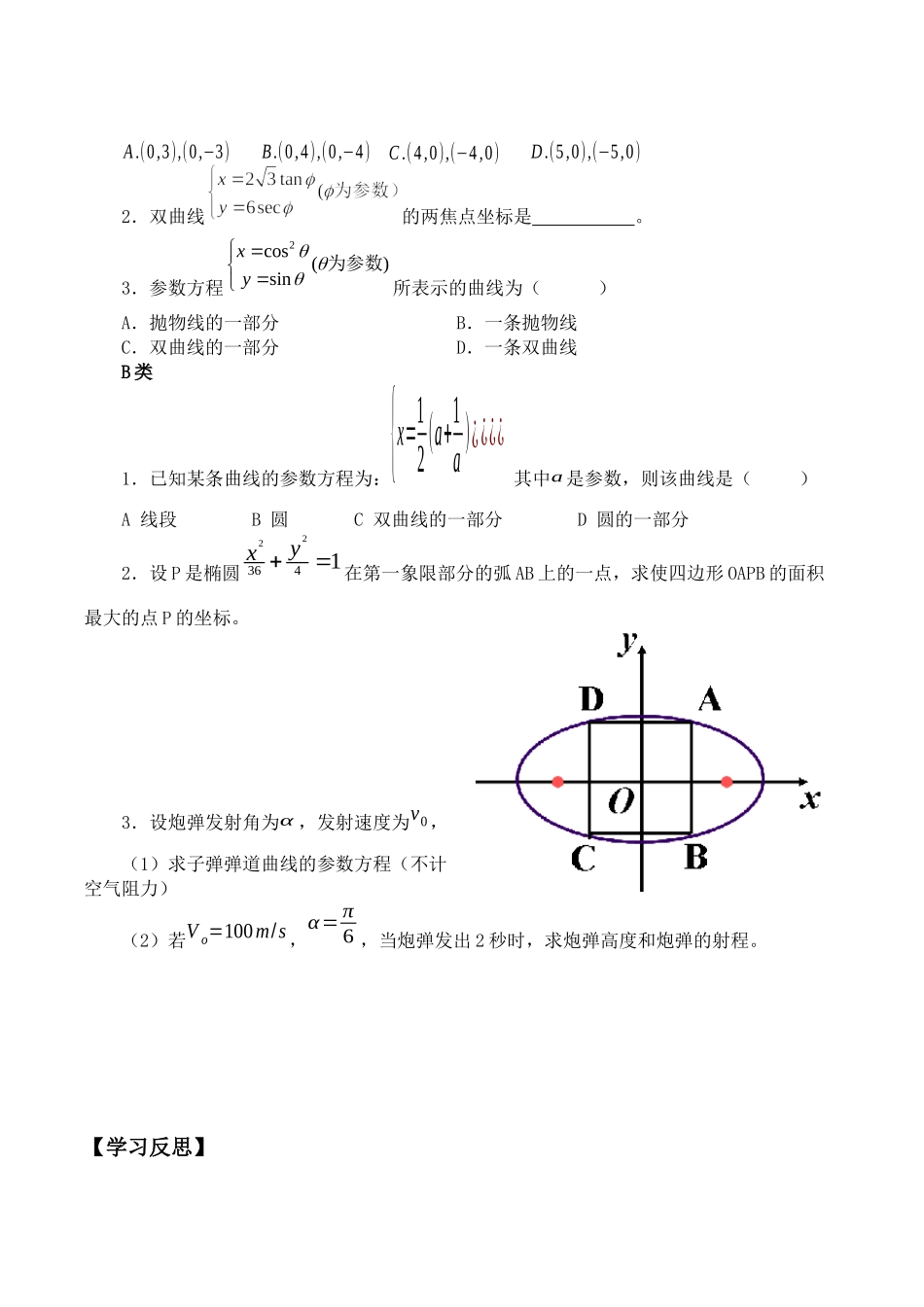
12222byax圆锥曲线的参数方程【学习目标】1.知识目标:了解圆锥曲线的参数方程及参数的意义。2.能力目标:能选取适当的参数,求简单曲线的参数方程。3.德育目标:通过观察、探索、发现的创造性过程,培养创新意识。【学习重难点】圆锥曲线的参数方程的定义和方法。【知识链接】复习1:圆的参数方程及参数的几何意义是什么?圆x2+y2=r2(r>0)的参数方程:圆(x-a)2+(y-b)2=r2的参数方程:其中参数的几何意义为:复习2:圆的参数方程是怎样推导出来的呢?【学习指导】分组讨论学习法、探究式【学习过程】一、自主学习:(预习)椭圆的参数方程为的几何意义是什么?双曲线的参数方程为________________________抛物线的参数方程是_____________________,其中t=1tana二、合作探究:参数方程的推导过程是怎样的?三、巩固练习A类1.椭圆的两个焦点坐标是()x2a2+y2b2=1(a>b>0)a,b,ϕ{x=3cosϕ¿¿¿¿2.双曲线的两焦点坐标是。3.参数方程2cos()sinxy为参数所表示的曲线为()A.抛物线的一部分B.一条抛物线C.双曲线的一部分D.一条双曲线B类1.已知某条曲线的参数方程为:{x=12(a+1a)¿¿¿¿其中a是参数,则该曲线是()A线段B圆C双曲线的一部分D圆的一部分2.设P是椭圆223641yx在第一象限部分的弧AB上的一点,求使四边形OAPB的面积最大的点P的坐标。3.设炮弹发射角为α,发射速度为v0,(1)求子弹弹道曲线的参数方程(不计空气阻力)(2)若Vo=100m/s,α=π6,当炮弹发出2秒时,求炮弹高度和炮弹的射程。【学习反思】D.(5,0),(−5,0)B.(0,4),(0,−4)A.(0,3),(0,−3)C.(4,0),(−4,0)本节课我有什么收获:我还有哪些疑问:在今后的学习中我还有注意什么:【达标检测】1.参数方程表示的曲线是()A.x轴的上方B.x轴的下方C.y轴的右方D.y轴的左方2.已知点A(1,2),过点(5,-2)的直线与抛物线24yx交于另外两点B.C,那么,三角形ABC是()A.锐角三角形B.钝角三角形C.直角三角形D.答案不确定3.参数方程|cossin|22(02)12xy(1+sin)表示()A.双曲线的一支,这支过点1(1,)2B.抛物线的一部分,这部分过点1(1,)2C.双曲线的一支,这支过点1(1,)2D.抛物线的一部分,这部分过点1(1,)24.设M为抛物线22yx上的动点,给定点0(1,0)M,点P分线段0MM的比为2:1,则点P的轨迹方程为。5.已知椭圆{x=3cosθ¿¿¿¿(θ为参数),求(1)θ=π6时对应的点P的坐标(2)直线...