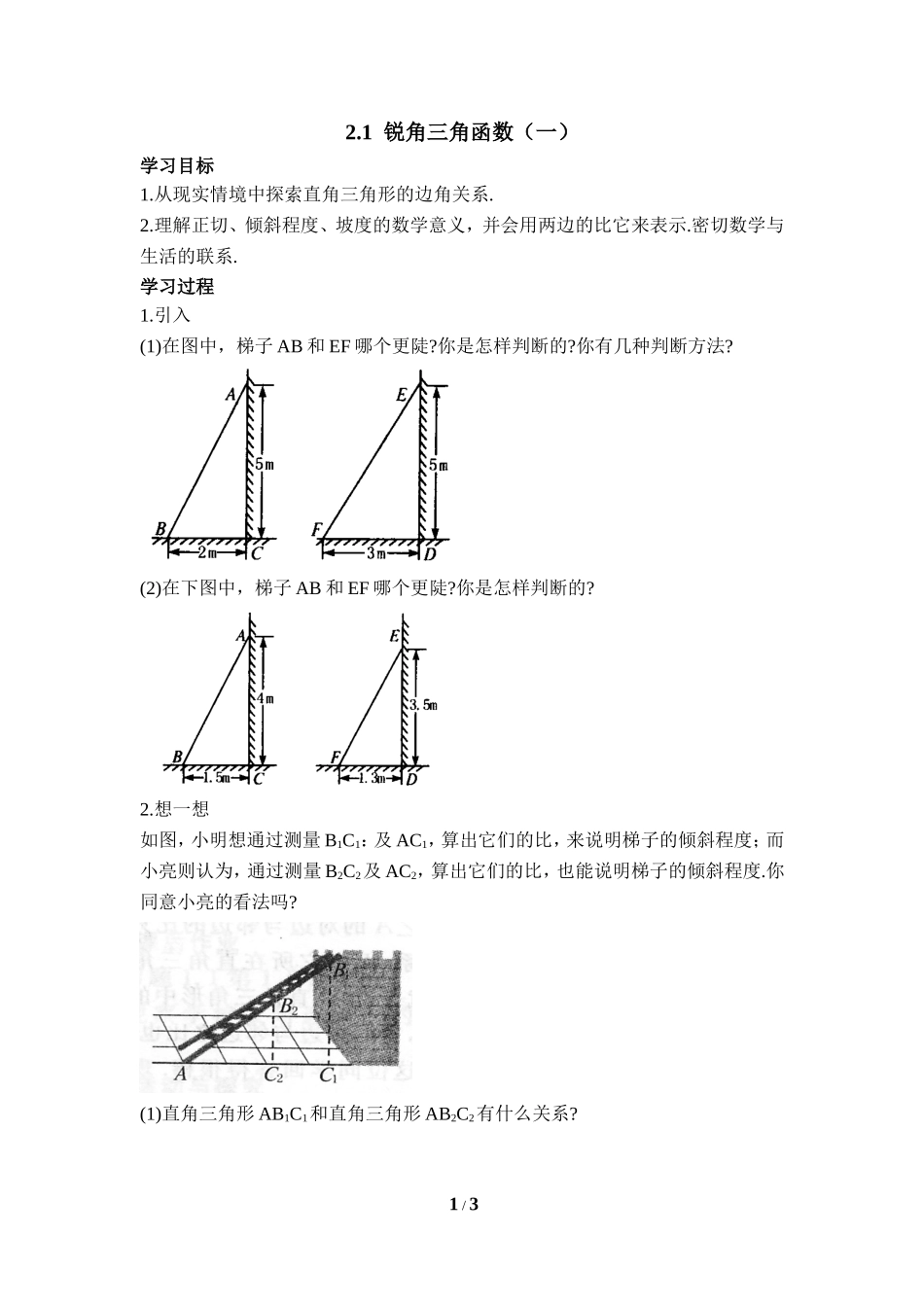
2.1锐角三角函数(一)学习目标1.从现实情境中探索直角三角形的边角关系.2.理解正切、倾斜程度、坡度的数学意义,并会用两边的比它来表示.密切数学与生活的联系.学习过程1.引入(1)在图中,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法?(2)在下图中,梯子AB和EF哪个更陡?你是怎样判断的?2.想一想如图,小明想通过测量B1C1:及AC1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?(1)直角三角形AB1C1和直角三角形AB2C2有什么关系?1/3(2)和有什么关系?(3)如果改变B2在梯子上的位置呢?由此你能得出什么结论?3.正切的定义由于直角三角形中的锐角A确定以后,它的对边与邻边之比也随之确定,因此我们有如下定义:在RtABC△中,如果锐角A确定,那么叫做∠A的正切(tangent),记作tanA,即tanA=思考:∠B的正切如何表示?它的数学意义是什么?如图,有一山坡在水平方向上每前进100m,就升高60m,那么山坡的坡度即坡角α的正切.[例1]如图是甲,乙两个自动扶梯,哪一个自动扶梯比较陡?[例2]在△ABC中,∠C=90°,BC=12cm,AB=20cm,求tanA和tanB的值.随堂练习1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗?2/3ABC∠A的对边∠A的邻边斜边2.菱形的两条对角线分别是16和12.较长的一条对角线与菱形的一边的夹角为θ,则tanθ=______.3/3