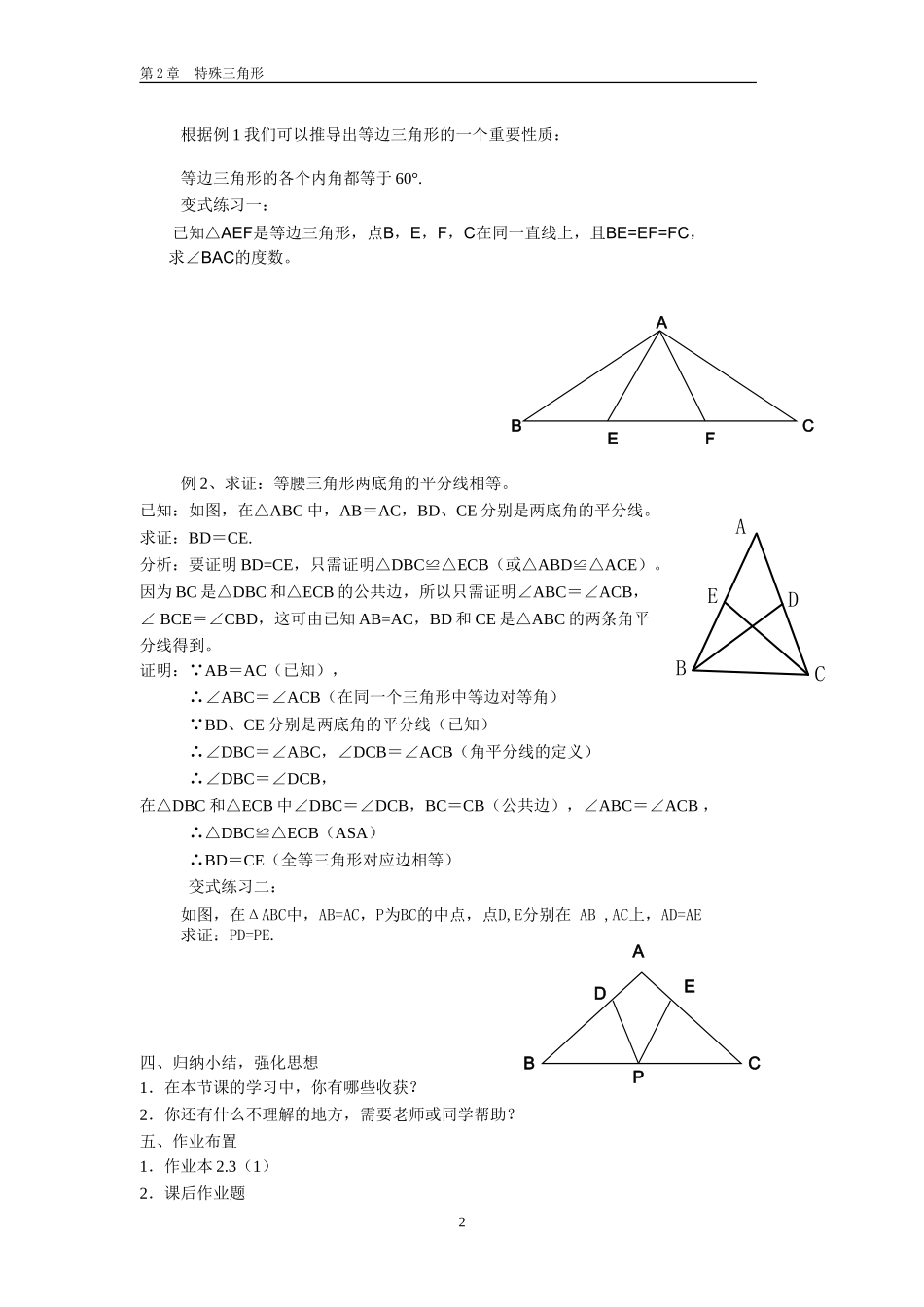
第2章特殊三角形2.3等腰三角形性质定理(1)〖教学目标〗◆1、经历根据等腰三角形的轴对称变换性发现等腰三角形性质的过程.◆2、掌握等腰三角形的性质定理1:等腰三角形的两个底角相等.◆3、会利用等腰三角形的性质定理1进行简单的推理、判断、计算和作图.◆4、探索等边三角形的性质:等边三角形的各个内角都等于60°.〖教学重点与难点〗◆教学重点:等腰三角形性质定理1.◆教学难点:等腰三角形性质定理1的证明需添加辅助线,思路较难形成,是本节教学的难点。〖教学过程〗一、创设情境,引入新课温故检测:叫做等腰三角形;等腰三角形是轴对称图形,它的对称轴是。[两边相等的三角形叫做等腰三角形。特殊情况是正三角形。对称轴是等腰三角形顶角平分线所在的直线。]二、合作交流,探求新知1.等腰三角形的性质合作学习:分三组教学活动材料教学活动材料1:如图2-5,在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D。(1)把这个等腰三角形剪下来,然后沿着顶角平分线对折,仔细观察重合的部分,并写出所发现的结论。(2)你发现了等腰三角形的哪些性质?2.多媒体演示:教师借助媒体的动态效果,介绍在一个三角形中,等边对等角和三角形一边上中线、高线及角平分线的相对位置,帮助学生在理解的基础上,掌握等腰三角形的性质。3.试一试(1)在△ABC中,AB=AC,外角∠ACD=100°,则∠B=______。(2)等腰三角形的一个底角是70°,则其顶角度数为_________。(3)如果等腰三角形的一个内角等于70°,那么它的底角度数为__________。(4)如果等腰三角形中一个角是另一个角的两倍,那么它的底角度数为__________。三、例题学习,当堂练习例1、求等边三角形ABC三个内角的度数.分析:本题可直接应用等腰三角形定理1来解答。注:讲解时着重做好表述的板书示范。1CAB第2章特殊三角形根据例1我们可以推导出等边三角形的一个重要性质:等边三角形的各个内角都等于60°.变式练习一:已知△AEF是等边三角形,点B,E,F,C在同一直线上,且BE=EF=FC,求∠BAC的度数。例2、求证:等腰三角形两底角的平分线相等。已知:如图,在△ABC中,AB=AC,BD、CE分别是两底角的平分线。求证:BD=CE.分析:要证明BD=CE,只需证明△DBC≌△ECB(或△ABD≌△ACE)。因为BC是△DBC和△ECB的公共边,所以只需证明∠ABC=∠ACB,∠BCE=∠CBD,这可由已知AB=AC,BD和CE是△ABC的两条角平分线得到。证明: AB=AC(已知),∴∠ABC=∠ACB(在同一个三角形中等...