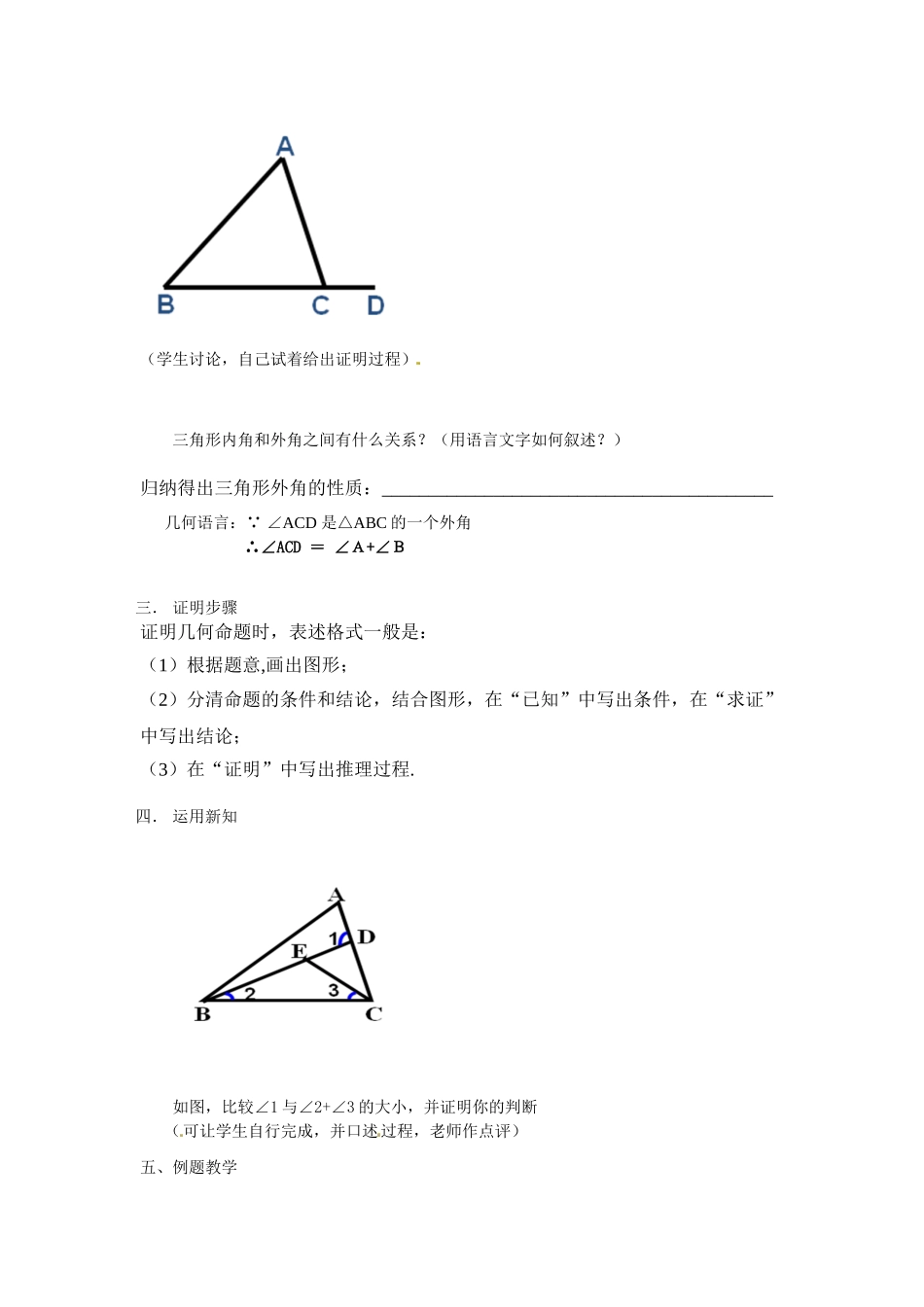
1.3证明(2)【教学目标】1.进一步体会证明的含义;2.探索并理解三角形内角和定理的几何证明;3.进一步熟练证明的方法和表述;4.让学生体验从实验几何向推理几何的过渡.【教学重点、难点】重点:探索三角形内角和定理的证明,进一步掌握证明的方法和表述.难点:如何添加辅助线解决问题及证明的表述【教学过程】[来源:学科网ZXXK]一、引例教学我们知道“三角形的内角和为180°”,你能证明吗?结合图形,先给出已知条件和结论,再证明这个定理。分析:(1)这个命题的条件和结论是什么?(2)请同学们回顾,在三角形部分,对这个命题是用哪种实验方法加以说明的.(可请成绩较好的同学回答)(3)请同学们思考:如何通过添加辅助线的方法把三个角拼在一起,这些线中哪些线容易产生相等的角?(同学之间相互合作,讨论学习,时间可稍长)根据学生的回答,添辅助线并引导学生梳理推理的过程(此处可引导学生在不同的顶点处添加辅助线)(4)师生共同完成推理过程.二.探索新知教师演示画图,给出外角概念1通过对三角形的外角的概念的理解,画出△ABC的外角,你能画出几个?2如图,∠ACD是△ABC的外角,求证:∠ACD=∠A+∠B已知:________________________________________________求证:______________________________________________证明:(提示:已知书写命题的条件,求证书写命题的结论,证明部分书写解题过程)(学生讨论,自己试着给出证明过程)[来三角形内角和外角之间有什么关系?(用语言文字如何叙述?)源:学科网]归纳得出三角形外角的性质:__________________________________________几何语言: ∠ACD是△ABC的一个外角∴∠ACD=∠A+∠B三.证明步骤证明几何命题时,表述格式一般是:(1)根据题意,画出图形;(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;(3)在“证明”中写出推理过程.四.运用新知如图,比较∠1与∠2+∠3的大小,并证明你的判断(可让学生自行完成,并口述过程,老师作点评)五、例题教学例4:已知,如图,∠B+∠D=∠BCD.求证:AB∥DE.证明:分析:要想证明平行通常有哪些方法?你能在图中找到证明AB∥DE的内错角,同位角或同旁内角吗?那么我们可以如何构造与这两直线有关的内错角,同位角或同旁内角呢?已知条件∠B+∠D=∠BCD有什么作用呢?什么图形中也存在这种形式的三角之间的等量关系呢?那么我们可以尝试怎么添辅助线呢?归纳:三种不同辅助线添...